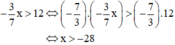PT \(\Leftrightarrow\dfrac{x^2+x+1-3x^2-2x^2+2x}{\left(x-1\right)\left(x^2+x+1\right)}=0\left(x\ne1\right)\)
\(\Leftrightarrow-4x^2+3x+1=0\)
\(\Leftrightarrow-4x^2+4x-x+1=0\)
\(\Leftrightarrow-4x\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(ktm\right)\\x=-\dfrac{1}{4}\left(TMx\ne1\right)\end{matrix}\right.\)
\(\dfrac{1}{x-1}-\dfrac{3x^2}{x^3-1}=\dfrac{2x}{x^2+x+1}\)
ĐKXĐ: x≠1
<=> \(\dfrac{x^2+x+1}{x^3-1}-\dfrac{3x^2}{x^3-1}=\dfrac{2x^2-2x}{x^3-1}\)
=> x2+x+1-3x2=2x2-2x
<=> x2-2x2+x+2x-3x2=-1
<=> -4x2+3x-1=0 <=> 4x2-3x+1=0
<=> 4x2-2.2x.\(\dfrac{3}{4}\)+\(\dfrac{9}{16}+\dfrac{7}{16}\)=0
<=> (2x-\(\dfrac{3}{4}\))2=-\(\dfrac{7}{16}\) (KTMĐK)
Vậy phương trình vô nghiệm




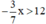 . Ta có:
. Ta có: