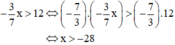2)\(\dfrac{x+5}{3x-6}-\dfrac{1}{2}=\dfrac{2x-3}{2x-4}\)
⇔\(\dfrac{x+5}{3\left(x-2\right)}-\dfrac{1}{2}=\dfrac{2x-3}{2\left(x-2\right)}\)
⇔\(\dfrac{2\left(x+5\right)}{3.2\left(x-2\right)}-\dfrac{3\left(x-2\right)}{2.3\left(x-2\right)}=\dfrac{3\left(2x-3\right)}{2.3\left(x-2\right)}\)
⇔\(\dfrac{2x+10}{6\left(x-2\right)}-\dfrac{3x-6}{6\left(x-2\right)}=\dfrac{6x-9}{6\left(x-2\right)}\)
⇔\(2x+10-\left(3x-6\right)=6x-9\)
⇔\(2x+10-3x+6-6x+9=0\)
⇔\(-7x+25=0\)
⇔\(-7x=-25\)
⇔\(x=\dfrac{25}{7}\)
3)\(\dfrac{1}{x-1}-\dfrac{3x^2}{x^3-1}=\dfrac{2x}{x^2+x+1}\)
⇔\(\dfrac{1}{x-1}-\dfrac{3x^2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{2x}{x^2+x+1}\)
⇔\(\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{3x^2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
⇔\(x^2+x+1-3x^2=2x^2-2x\)
⇔\(x^2+x+1-3x^2-2x^2+2x=0\)
⇔\(-4x^2+3x+1=0\)
⇔\(-\left(4x^2-3x-1\right)=0\)
⇔\(-\left(4x^2-4x+x-1\right)=0\)
⇔\(-\left[\left(4x^2-4x\right)+\left(x-1\right)\right]=0\)
⇔\(-\left[4x\left(x-1\right)+\left(x-1\right)\right]=0\)
⇔\(-\left[\left(x-1\right)\left(4x+1\right)\right]=0\)
⇔\(-\left(x-1\right)=0\) hay \(-\left(4x+1\right)=0\)
⇔\(-x+1=0\) hay \(-4x-1=0\)
⇔\(-x=-1\) hay \(-4x=1\)
⇔\(x=1\) hay \(x=-\dfrac{1}{4}\)



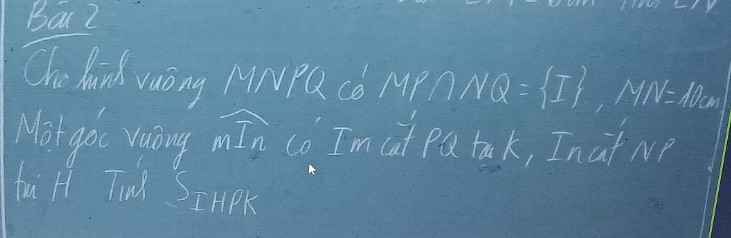
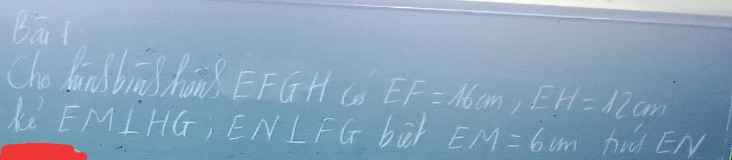
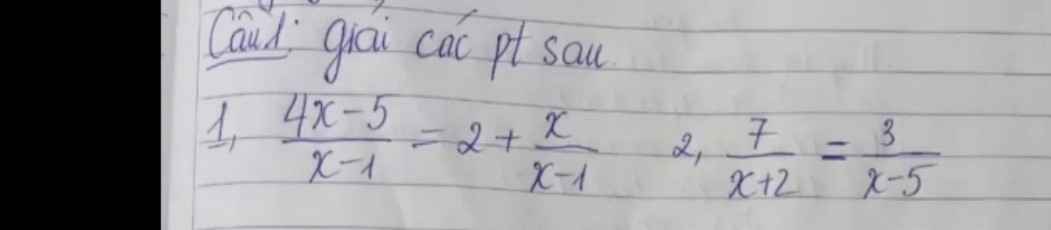
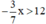 . Ta có:
. Ta có: