Điều kiện x ≠ kπ ∀ k ∈ Z
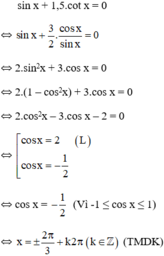
Vậy phương trình có tập nghiệm
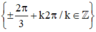
Điều kiện x ≠ kπ ∀ k ∈ Z
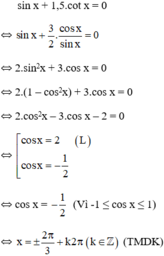
Vậy phương trình có tập nghiệm
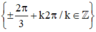
Giải các phương trình sau cos2x - sinx - 1 = 0
Giải các phương trình sau: 1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0
Giải phương trình lượng giác sau:
\(\dfrac{cos2x}{1-sinx}=0\)
Giải phương trình 2sinx – 3 = 0 là phương trình bậc nhất đối với sinx.
Giải phương trình cos x - 3 . sin x 2 . sin x - 1 = 0
![]()
![]()
![]()
![]()
Giải phương trình sin2x - 12(sinx - cosx) + 12 = 0
![]()
![]()
![]()
Giải phương trình: sinx + cosx + 1 + sin2x + cos2x = 0
![]()
![]()
![]()
![]()
Giải phương trình sin3x(cosx - 2sin3x) + cos3x(1 + sinx - 2cos3x) = 0
A. x = ± π 3 + k2π, k ∈ Z
B. x = π 4 + kπ, k ∈ Z
C. x = - π 4 + k2π, x = - π 6 + k2π,k ∈ Z
D. Vô nghiệm
Giải phương trình sau: sin x + 1 = 2 3