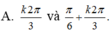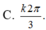\(\Leftrightarrow2\sin3x=1\)
\(\Leftrightarrow\sin3x=\dfrac{1}{2}\)
\(\Leftrightarrow\sin3x=\dfrac{\pi}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=\dfrac{\pi}{6}+k2\pi\\3x=\pi-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{18}+k\dfrac{\pi}{2}\\x=\dfrac{5\pi}{18}+k\dfrac{\pi}{3}\end{matrix}\right.\left(k\in Z\right)\)
\(\Leftrightarrow2sin3x=1\)
\(\Leftrightarrow2sin3x=sin1\)
\(\Leftrightarrow sin3x=sin\dfrac{1}{2}\)
\(\Leftrightarrow sin3x=sin\dfrac{\Pi}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=\dfrac{\Pi}{6}+K2\Pi\\3x=\Pi-\dfrac{\Pi}{6}+K2\Pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{18}+K\dfrac{2\Pi}{3}\\3x=\dfrac{5\Pi}{6}+K2\Pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{18}+K\dfrac{2\Pi}{3}\\x=\dfrac{5\Pi}{18}+K\dfrac{2\Pi}{3}\end{matrix}\right.\left(K\in Z\right)\)