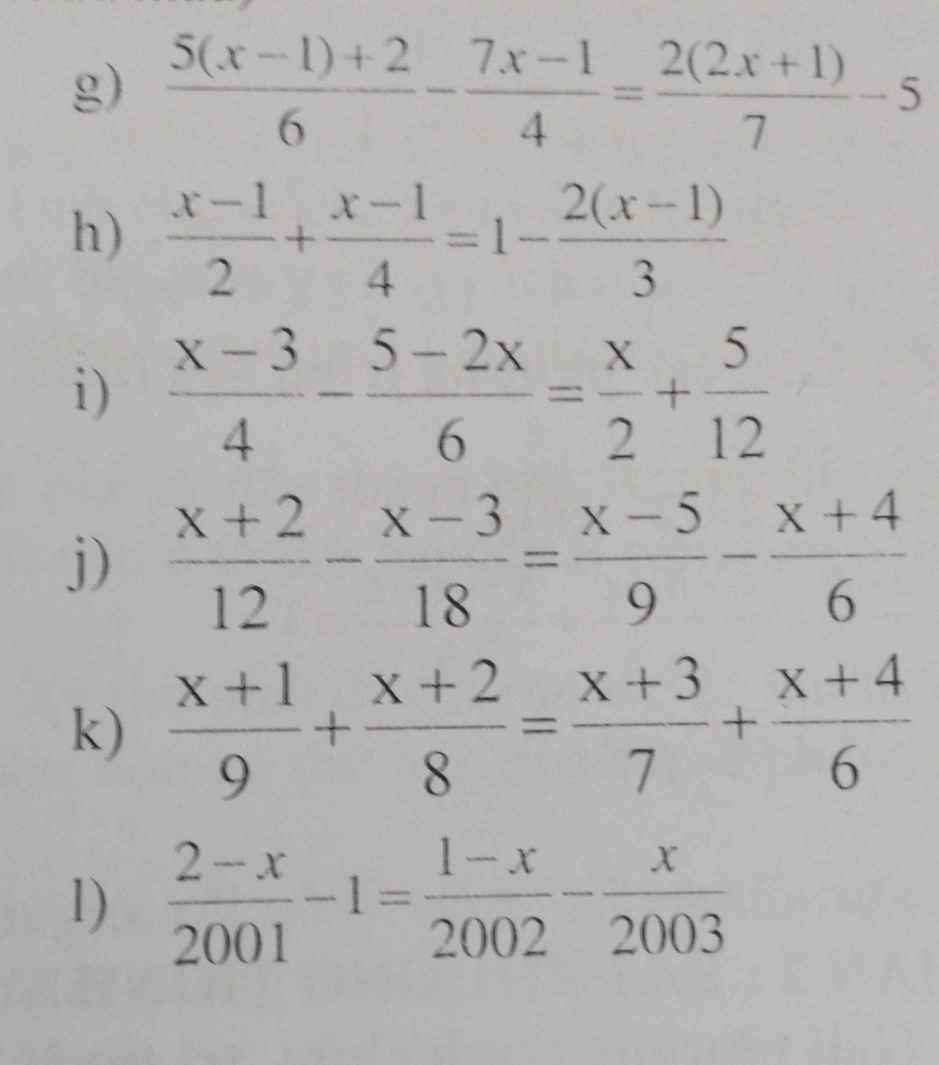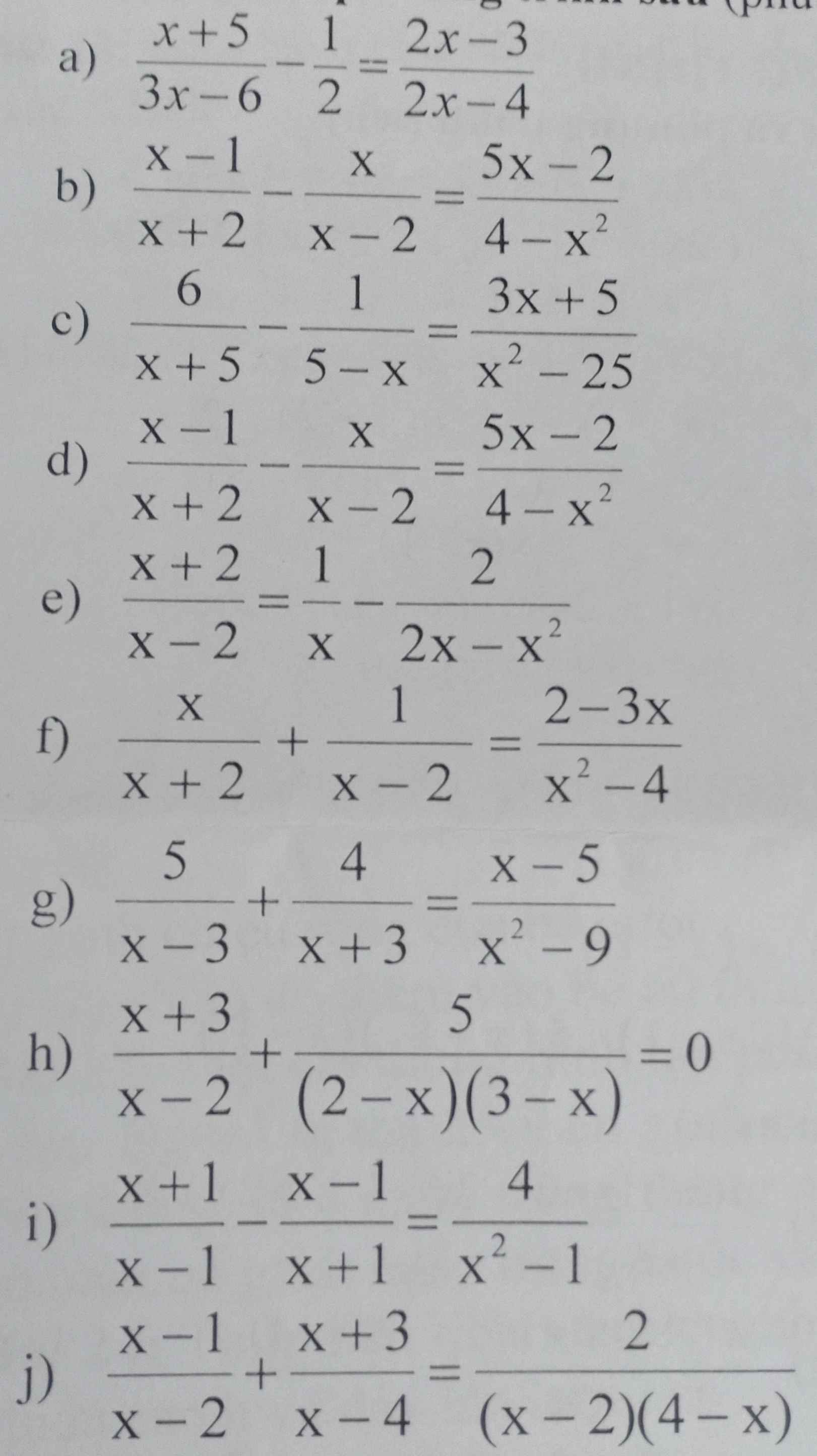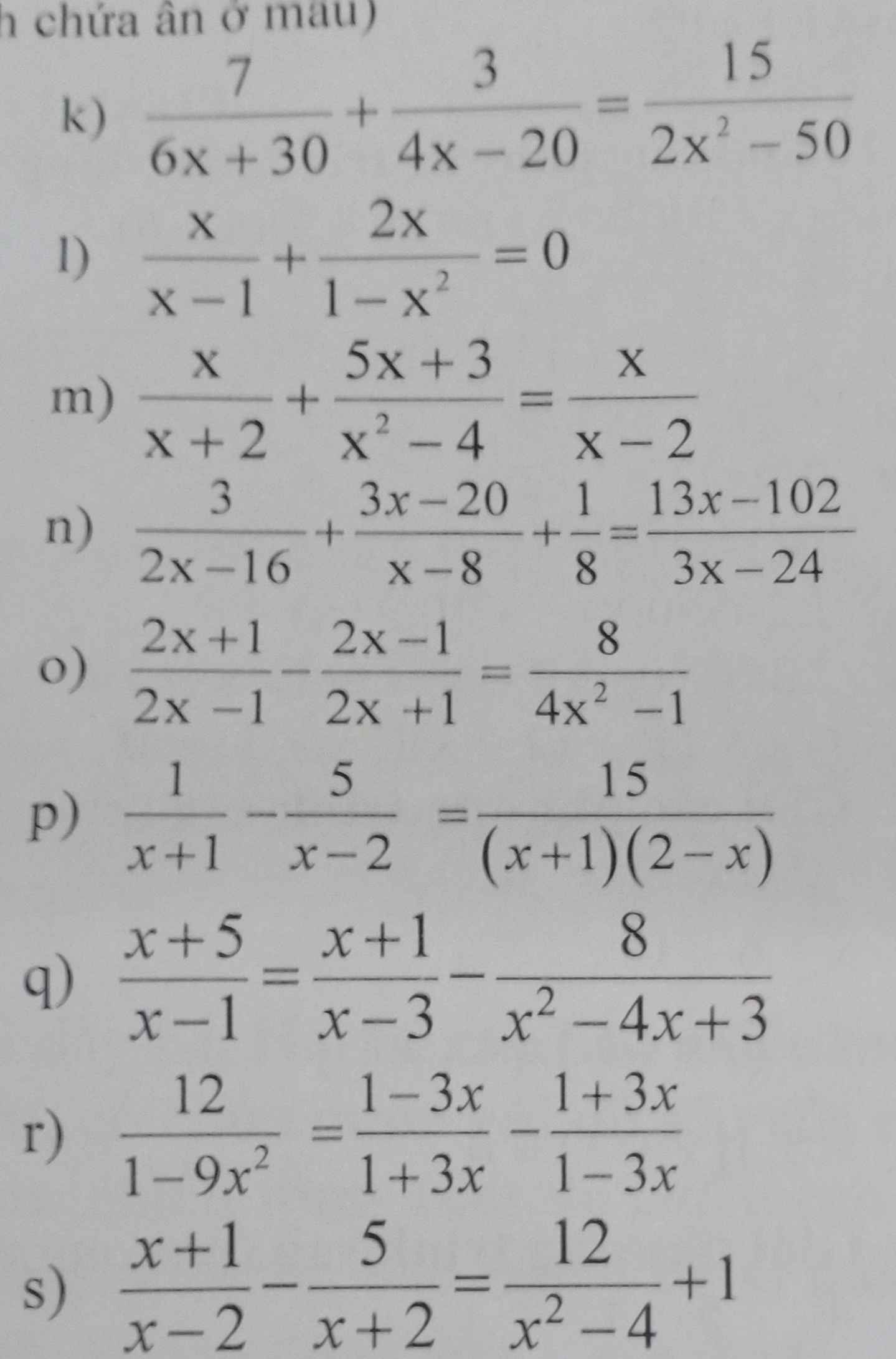a) Xét △ vuông ACH và △ vuông BCA, ta có:
∠C chung
∠CHA = ∠CAB (=90 độ)
⇒ △ vuông ACH ∼ △ vuông BAC (g.g)
b)
+)Theo định lý py-ta-go, ta có:
BC2 = AB2 + AC2
⇒ BC = \(\sqrt{AB^2+AC^2}\)= \(\sqrt{20^2+15^2}\)= 25cm
+) Vì △ vuông ACH ∼ △ vuông BCA (c/ma)
⇒\(\dfrac{AC}{BC}=\dfrac{AH}{BA}\)⇔\(\dfrac{15}{25}=\dfrac{AH}{20}\)⇔25AH = 300 ⇔ AH = 12cm
Đúng 0
Bình luận (1)



 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !