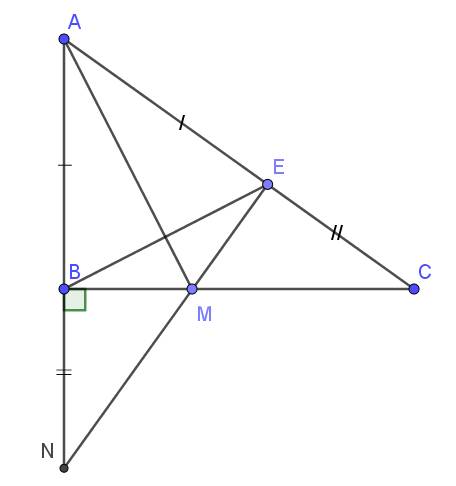
Lời giải:
a. Xét tam giác $ABM$ và $AEM$ có:
$AB=AE$ (gt)
$AM$ chung
$\widehat{BAM}=\widehat{EAM}$ (do $AM$ là phân giác $\widehat{BAC}$)
$\Rightarrow \triangle ABM=\triangle AEM$ (c.g.c)
b.
Từ tam giác bằng nhau phần a suy ra $AB=AE, MB=ME$
$\Rightarrow AM$ là trung trực của $BE$
$\Rightarrow AM\perp BE$
c.
Từ tam giác bằng nhau phần a suy ra $\widehat{MEA}=\widehat{MBA}=90^0$
$\Rightarrow ME\perp AC\Rightarrow \widehat{MEC}=90^0$
Xét tam giác $MBN$ và $MEC$ có:
$MB=ME$ (cmt)
$BN=EC$ (gt)
$\widehat{MBN}=\widehat{MEC}=90^0$
$\Rightarrow \triangle MBN=\triangle MEC$ (c.g.c)
$\Rightarrow \widehat{BMN}=\widehat{EMC}$
$\Rightarrow \widehat{BMN}+\widehat{BME}=\widehat{EMC}+\widehat{BME}$
$\Rightarrow \widehat{NME}=\widehat{BMC}=180^0$
$\Rightarrow M,E,N$ thẳng hàng.
 Giải gấp giúp mình với ạ
Giải gấp giúp mình với ạ