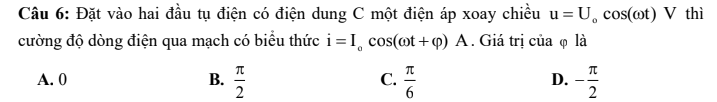Hệ thức độc lập thời gian:
\(\dfrac{x^2}{A^2}+\dfrac{v^2}{\left(\omega A\right)^2}=1\)
\(\Rightarrow A^2=x^2+\dfrac{v^2}{\omega^2}\) với \(\left\{{}\begin{matrix}A=\alpha_0\cdot l\\x=\alpha\cdot l\\\omega=\sqrt{\dfrac{g}{l}}\Rightarrow\omega^2=\dfrac{g}{l}\end{matrix}\right.\)
\(\Rightarrow\left(\alpha_0\cdot l\right)^2=\left(\alpha\cdot l\right)^2+\dfrac{v^2}{\dfrac{g}{l}}=\left(\alpha\cdot l\right)^2+\dfrac{v^2\cdot l}{g}\)
\(\Rightarrow\alpha_0^2=\alpha^2+\dfrac{v^2}{g\cdot l}\) do rút gọn \(l\)
\(\Rightarrow\alpha_0=\sqrt{\alpha^2+\dfrac{v^2}{g\cdot l}}\)
Chọn A.
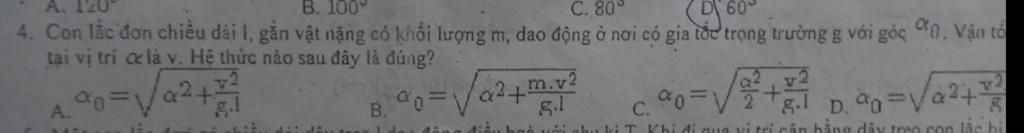





 giải chi tiết 3 bài này dùm em vs ạ
giải chi tiết 3 bài này dùm em vs ạ