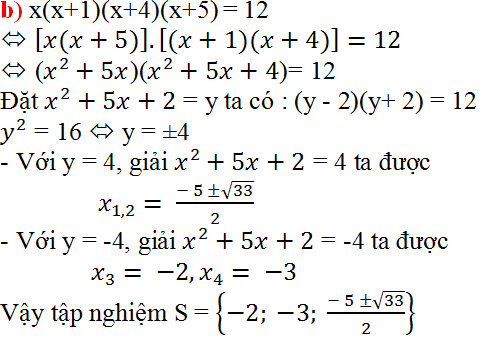a. \(2x^3-x^2+3x+6=0\)
\(\Leftrightarrow2x^3+2x^2-3x^2-3x+6x+6=0\)
\(\Leftrightarrow2x^2\left(x+1\right)-3x\left(x+1\right)+6\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x^2-3x+6\right)=0\)
\(\Leftrightarrow x+1=0\) ( vì \(2x^2-3x+6\) > 0 với mọi x)
\(\Leftrightarrow x=-1\)
Vậy tập nghiệm của pt là \(S=\left\{-1\right\}\).
b. \(x\left(x+1\right)\left(x+4\right)\left(x+5\right)=12\)
\(\Leftrightarrow\left(x^2+5x\right)\left(x^2+5x+4\right)=12\)(1)
Đặt \(x^2+5x=a\) . Khi đó pt (1) trở thành :
\(a\left(a+4\right)=12\)
\(\Leftrightarrow a^2+4a-12=0\)
\(\Leftrightarrow\left(a-2\right)\left(a+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-2=0\\a+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-6\end{matrix}\right.\)
* Với a = 2 thì \(x^2+5x=2\Leftrightarrow x^2+5x-2=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-5+\sqrt{33}}{2}\\x=\dfrac{-5-\sqrt{33}}{2}\end{matrix}\right.\)
* Với a = -6 thì \(x^2+5x=-6\Leftrightarrow x^2+5x+6=0\Leftrightarrow\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\)
Vậy tập nghiệm của pt là \(S=\left\{\dfrac{-5+\sqrt{33}}{2};\dfrac{-5-\sqrt{33}}{2};-2;-3\right\}\)