BPT\(\Leftrightarrow\left|x^2+3x+2\right|>2x-x^2\)
TH1:\(2x-x^2< 0\Leftrightarrow x\in R\backslash\left[0;2\right]\) (1)
TH2:\(\left\{{}\begin{matrix}2x-x^2\ge0\\\left(x^2+3x+2\right)^2>\left(2x-x^2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\in\left[0;2\right]\\\left(2x^2+x+2\right)\left(5x+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\in\left[0;2\right]\\5x+2>0\end{matrix}\right.\)\(\Rightarrow x\in\left[0;2\right]\) (2)
Từ (1) (2) suy ra \(x\in R\)
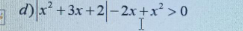 Giải bpt sau :
Giải bpt sau :
