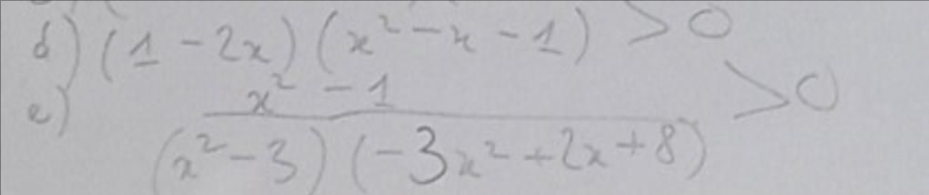d, $1-2x=0\Leftrightarrow x=\dfrac{1}{2}$
$x^2-x-1=0\Leftrightarrow x=\dfrac{1\pm\sqrt 5}{2}$
Bảng xét dấu:
\begin{array}{|c|cc|}\hline x&-\infty&&\dfrac{1-\sqrt 5}{2}&&\dfrac{1}{2}&&\dfrac{1+\sqrt 5}{2}&&+\infty\\\hline 1-2x&&+&|&+&0&-&|&-&\\\hline x^2-x-1&&+&0&-&|&-&0&+&\\\hline f(x)&&+&0&-&0&+&0&-&\\\hline\end{array}
$f(x)>0\Rightarrow x\in\left(-\infty;\dfrac{1-\sqrt 5}{2}\right)\cup\left(\dfrac{1}{2};\dfrac{1+\sqrt 5}{2}\right)$
Vậy $ x\in\left(-\infty;\dfrac{1-\sqrt 5}{2}\right)\cup\left(\dfrac{1}{2};\dfrac{1+\sqrt 5}{2}\right)$
e, $x^2-1=0\Leftrightarrow x=\pm 1$
$x^2-3=0\Leftrightarrow x=\pm\sqrt 3$
$-3x^2+2x+8=0\Leftrightarrow \left[\begin{array}{1}x=2\\x=-\dfrac{4}{3}\end{array}\right.$
Bảng xét dấu:
$\begin{array}{|c|cc|}\hline x&-\infty&&-\sqrt 3&&-\dfrac{4}{3}&&-1&&1&&\sqrt 3&&2&&+\infty\\\hline x^2-1&&+&|&+&|&+&0&-&0&+&|&+&|&+&\\\hline x^2-3&&+&0&-&|&-&|&-&|&-&0&+&|&+&\\\hline -3x^2+2x+8&&-&|&-&0&+&|&+&|&+&|&+&0&-&\\\hline f(x)&&-&||&+&||&-&0&+&0&-&||&+&||&-&\\\hline\end{array}$
$f(x)>0\Rightarrow x\in\left(-\sqrt 3;-\dfrac{4}{3}\right)\cup (-1;1)\cup (\sqrt 3;2)$
Vậy $x\in\left(-\sqrt 3;-\dfrac{4}{3}\right)\cup (-1;1)\cup (\sqrt 3;2)$