Các câu hỏi tương tự
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số yf(x) và trục hoành như hình vẽ bên. Đặt a
∫
-
1
1
f
(
x
)
d
x
,
b
∫
1
2
f
(
x
)
d
x
. Mệnh đề nào sau đây đúng ? A. Sa+b B. Sa-b C. S -a+b D. S-a-b
Đọc tiếp
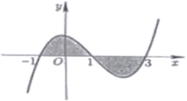
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) và trục hoành như hình vẽ bên. Đặt a= ∫ - 1 1 f ( x ) d x , b = ∫ 1 2 f ( x ) d x . Mệnh đề nào sau đây đúng ?

A. S=a+b
B. S=a-b
C. S= -a+b
D. S=-a-b
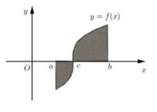
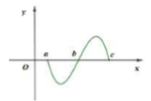
Cho hàm số y f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm a c (acb) (như hình vẽ bên). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y f(x) trục hoành và hai đường thẳng xa; xb Mệnh đề nào dưới đây đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm a = c (a<c<b) (như hình vẽ bên). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b Mệnh đề nào dưới đây đúng?
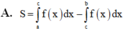
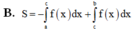
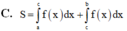
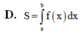
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
-
1
x
+
1
và các trục tọa độ. Khi đó giá trị của S bằng A. S ln2 - 1 (đvdt) B. S 2ln2 - 1 (đvdt) C. S 2ln2 + 1 (đvdt) D. S ln2 + 1 (đvdt)
Đọc tiếp
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x - 1 x + 1 và các trục tọa độ. Khi đó giá trị của S bằng
A. S = ln2 - 1 (đvdt)
B. S = 2ln2 - 1 (đvdt)
C. S = 2ln2 + 1 (đvdt)
D. S = ln2 + 1 (đvdt)
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
f
(
x
)
1
3
x
3
-
x
2
-
1
3
x
+
1
và trục hoành như hình vẽ bên. Mệnh đề nào sau đây sai?
Đọc tiếp
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số f ( x ) = 1 3 x 3 - x 2 - 1 3 x + 1 và trục hoành như hình vẽ bên. Mệnh đề nào sau đây sai?
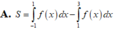
![]()
![]()
![]()
Cho hàm số
y
x
-
m
2
x
+
1
(với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S 1? A. Hai. B. Ba. C. Một. D. Không
Đọc tiếp
Cho hàm số y = x - m 2 x + 1 (với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S = 1?
A. Hai.
B. Ba.
C. Một.
D. Không
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số
y
x
3
, trục hoành và hai đường x-1, x2, biết rằng mỗi đơn vị dài trên các trục tọa độ là 2cm.
Đọc tiếp
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = x 3 , trục hoành và hai đường x=-1, x=2, biết rằng mỗi đơn vị dài trên các trục tọa độ là 2cm.
![]()
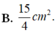
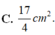
![]()
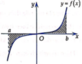
Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
f
(
x
)
trục hoành và đường thẳng xa;xb (như hình vẽ bên). Hỏi khẳng định nào dưới đây là khẳng định đúng?
Đọc tiếp
Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số = y = f ( x ) trục hoành và đường thẳng x=a;x=b (như hình vẽ bên). Hỏi khẳng định nào dưới đây là khẳng định đúng?
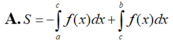
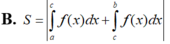
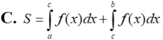
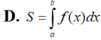
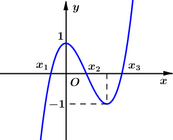
Cho hàm số bậc ba yf(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng...
Đọc tiếp
Cho hàm số bậc ba y=f(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
=
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng giới hạn bởi các đường
y
=
f
x
+
1
,
y
=
-
f
x
-
1
,
x
=
x
1
và
x
=
x
3
bằng![]()
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số yf(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị (C): yf(x), trục hoành và hai đường thẳng xa, yb (như hình vẽ dưới đây). Giả sử
S
D
là diện tích của hình phẳng D. Chọn công thức đúng trong các phương án dưới đây A.
S
D
−
∫
a
0
f
x
d
x
+
∫...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị (C): y=f(x), trục hoành và hai đường thẳng x=a, y=b (như hình vẽ dưới đây). Giả sử S D là diện tích của hình phẳng D. Chọn công thức đúng trong các phương án dưới đây
A. S D = − ∫ a 0 f x d x + ∫ 0 b f x d x .
B. S D = ∫ a 0 f x d x − ∫ 0 b f x d x .
C. S D = ∫ a 0 f x d x + ∫ 0 b f x d x .
D. S D = − ∫ a 0 f x d x − ∫ 0 b f x d x .


