Các câu hỏi tương tự
Giả sử F(x) là một nguyên hàm của
f
(
x
)
ln
(
x
+
3
)
x
2
sao cho F(-2)+F(1)0. Giá trị của F(-1)+F(2) bằng B. 0
Đọc tiếp
Giả sử F(x) là một nguyên hàm của f ( x ) = ln ( x + 3 ) x 2 sao cho F(-2)+F(1)=0. Giá trị của F(-1)+F(2) bằng
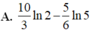
B. 0
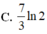
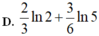
Cho hàm số
y
x
+
2
2
x
+
3
có đồ thị (C). Giả sử, đường thẳng d: ykx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác
∆
O
A
B
cân tại gốc tọa độ O. Tổng k+m có giá trị bằng: A. 1. B. 3. C. -1. D. -3.
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác ∆ O A B cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1.
D. -3.
Tìm giá trị dương của k để
lim
x
→
+
∞
(
3
k
+
1
)
x
2
+
1
x
9
f
(
2
)
với ...
Đọc tiếp
Tìm giá trị dương của k để lim x → + ∞ ( 3 k + 1 ) x 2 + 1 x = 9 f ' ( 2 ) với f ( x ) = ln ( x 2 + 5 )
A. k = 12
B. k = 2
C. k = 5
D. k = 9
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số
f
x
1
1
+
sinx
a) F(x) 1 -
cos
x
2
+
π
4...
Đọc tiếp
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số f x = 1 1 + sinx
a) F(x) = 1 - cos x 2 + π 4
b) G(x) = 2 tan x 2
c) H(x) = ln(1 + sinx)
d) K(x) = 2 1 - 1 1 + tan x 2
Tính giá trị bằng số của biểu thức 4 log 2 3
A. 81 B. 9
C. 1/3 D. 1/27
Tính giá trị bằng số của biểu thức 4 log 2 3
A. 81 B. 9
C. 1/3 D. 1/27
Giải các bất phương trình sau:a) (2x − 7)ln(x + 1) 0;b) (x − 5)(logx + 1) 0;c) 2
log
3
2
x
+ 5
log
2
2
x
+
log
2
x
– 2 ≥ 0d) ln(3
e
x
− 2) ≤ 2x
Đọc tiếp
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
n là số nguyên dương và k là tích của tất cả các số nguyên từ 1 đến n. Nếu k là bội số của 1440 thì giá trị nhỏ nhất có thể có của n là A. 8 B. 12 C. 16 D. 18 E. 24
Cho hàm số y x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y 0 là A. 1 B. 2 C. 3 D. không có giá trị nào của m thỏa mãn
Đọc tiếp
Cho hàm số y= x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y= 0 là
A. 1
B. 2
C. 3
D. không có giá trị nào của m thỏa mãn


