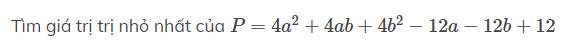\(P=4a^2+4ab+4b^2-12a-12b+12\)
\(=\left(2a\right)^2+4a\left(b-3\right)+\left(b-3\right)^2-\left(b^2-6b+9\right)+4b^2-12b+12\)
\(=\left(2a+b-3\right)^2+3b^2-6b+3\)
\(=\left(2a+b-3\right)^2+3\left(b-1\right)^2\)
Vì \(\left(2a+b-3\right)^2\ge0;3\left(b-1\right)^2\ge0\) với mọi x
=> P>=0 với mọi x
Dấu bằng xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}2a+b-3=0\\b-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)
Vậy, \(P_{max}=0\Leftrightarrow a=b=1\)