Đáp án A.
Ta có
F x = ∫ 3 x 2 + 1 2 x + 1 d x = x 3 + 1 2 ln 2 x + 1 + C
mà F 0 = 0 ⇒ C = 0
Do đó
F x = x 3 + 1 2 ln 2 x + 1 ⇒ F 1 = 1 + 1 2 ln 3 ⇒ a = 1 ; b = 1 ; c = 2 ⇒ a + b + c = 4 .
Đáp án A.
Ta có
F x = ∫ 3 x 2 + 1 2 x + 1 d x = x 3 + 1 2 ln 2 x + 1 + C
mà F 0 = 0 ⇒ C = 0
Do đó
F x = x 3 + 1 2 ln 2 x + 1 ⇒ F 1 = 1 + 1 2 ln 3 ⇒ a = 1 ; b = 1 ; c = 2 ⇒ a + b + c = 4 .
Cho f(x) là hàm liên tục trên đoạn 0 ; a thỏa mãn f x f a − x = 1 f x > 0 , ∀ x ∈ 0 ; a và ∫ 0 a d x 1 + f x = b a c , trong đó b, c là hai số nguyên dương và b c là phân số tối giản. Khi đó b + c có giá trị thuộc khoảng nào dưới đây?
A. 11 ; 22
B. 0 ; 9
C. 7 ; 21
D. 2017 ; 2020
Cho hàm số f (x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) và f ' ( x ) = 1 x 2 + x , f ( 1 ) = ln 1 2 . Biết ∫ 1 2 ( x 2 + 1 ) f ( x ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị biểu thức a+b+c bằng
A. 27 2
B. 1 6
C. 7 6
D. - 3 2
Cho hàm số y = f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tập tất cả các giá trị của m để đồ thị hàm số y = f x có 5 điểm cực trị là a b ; c với a, b, c là các số nguyên và a b là phân số tối giản. Tính a+b+c
A. 11
B. 8
C. 10
D. 5
Cho hàm số f(x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) thỏa mãn f ' ( x ) = 1 x 2 + x , f ( 1 ) = ln 1 2 . Cho ∫ 1 2 ( x 2 + 1 ) 2 f ( x ) d x =a ln3+b ln2+c, với a,b,c là các số hữu tỷ. Giá trị biểu thức a+b+c bằng
A. 27 20
B. 23 20
C. - 27 20
D. - 23 20
Biết F (x) là một nguyên hàm của hàm số f ( x ) = 10 x 3 - 7 x + 2 2 x - 1 thỏa mãn F(1) = 5. Giả sử rằng F(3) = a + b 5 , trong đó a , b là các số nguyên. Tính tổng bình phương của a và b.
A. 121
B. 73
C. 265
D. 361
Tìm nguyên hàm của hàm số f ( x ) = 2008 + ln 2 x x có
dạng F ( x ) = a ln x + ln x 3 b + C . Khi đó tổng S
= a + b là?
A. 2012
B. 2010
C. 2009
D. 2011
Biết hàm số F ( x ) = a x 3 + ( a + b ) x 2 + ( 2 a - b + c ) x + 1 là một nguyên hàm của hàm số f ( x ) = 3 x 2 + 6 x + 2 . Tổng a+b+c là:
A. 5
B. 4
C. 3
D. 2
Biết F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của hàm số f ( x ) = ( 2 x 2 - 5 x + 2 ) e - x trên R. Giá trị của biểu thức f(F(0)) bằng
A. 9e
B. 3e
C. 20 e 2
D. - 1 e
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số y = f ’ ( x ) cho bởi hình vẽ. Giá trị f ( 3 ) - 2 f ( 1 ) là
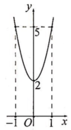
A. 30
B. 24
C. 26
D. 27