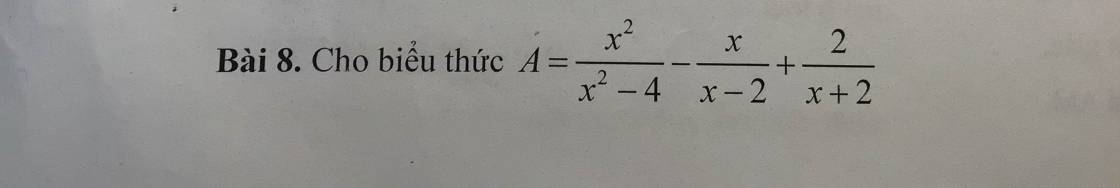Question

Ét o éttt còn ai thức ko ạ giúp mik bài này với ạ, mai mik học rồi  cho mik câu trả lời chi tiết rõ ràng nhất với xong mik sẽ tick, mik cảm ơn nhiều ạ 🤧

Answer 1

\(A=\dfrac{x^2}{x^2-4}-\dfrac{x}{x-2}+\dfrac{2}{x+2}\)
\(A=\dfrac{x^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x}{x-2}+\dfrac{2}{x+2}\)

\(A=\dfrac{x^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)

\(A=\dfrac{x^2-x^2-2x+2x-4}{\left(x-2\right)\left(x+2\right)}\)

\(A=\dfrac{-4}{\left(x-2\right)\left(x+2\right)}\)

Answer 2

\(\dfrac{x^2}{x^2-4}-\dfrac{x}{x-2}+\dfrac{2}{x+2}\\ =\dfrac{x^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x}{x-2}+\dfrac{2}{x+2}\\ =\dfrac{x^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{x^2-x\left(x+2\right)+2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{x^2-x^2-2x+2x-4}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{-4}{\left(x-2\right)\left(x+2\right)}\)