Ta có: a2= 16; b2= 12 nên c2= 16-12= 4
=> c = 2
Đường chuẩn .
![]()
Chọn D.
Ta có: a2= 16; b2= 12 nên c2= 16-12= 4
=> c = 2
Đường chuẩn .
![]()
Chọn D.
Cho elip 3x2 + 4y2 – 48 = 0 và đường thẳng d: x - 2y + 4 = 0. Giao điểm của d và Elip là
A. (0; - 4); (-2; -3) B. (4; 0); (3; 2) C. (0; 4); (-2; 3) D. (-4; 0); (2; 3)
Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi 2 đường thẳng ∆ 1: x+ 2y -3= 0 và ∆2: 2x – y + 3= 0.
A. x+ 3y-2= 0 và x= 3y.
B. 3x= - y và x-3y-6= 0.
C. 3x+ y= 0 và –x+ 3y- 6= 0.
D.Đáp án khác
Bài 1: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua đường thẳng Δ, với:
a, d: 2x-y+1=0, Δ: 3x-4y+2=0
b, d: x-2y+4=0, Δ: 2x+y-2=0
c, d: x+y-1=0, Δ: x-3y+3=0
d, d: 2x-3y+1=0, Δ: 2x-3y-1=0
Bài 2: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua điểm I với:
a, d: 2x-y+1=0, I(2;1)
b, d: x-2y+4=0, I(-3;0)
c, d: x+y-1=0, I(0:3)
d, d: 2x-3y+1=0, I trùng O(0;0)
GIÚP EM VỚI Ạ!! EM ĐANG CẦN GẤP LẮM HUHUU T^T EM XIN CẢM ƠN!!!
Phần 1: Đại số
Câu 1 (2đ): Xét dấu các biểu thức sau:
a.
f x x 3 4
; c.
2
f x x x x 1 2 5 2 .
b.
2
f x x x 9 6 1
; d.
2
2 5
2
x
f x
x x
.
Câu 2 (4đ): Giải các bất phương trình sau:
a.
2
3 4 4 0 x x
; c.
2
1 2 5
0
3
x x
x
.
b.
2
2 4 4 0 x x x
; d.
2
2
5 2 3
0
2
x x
x x
.
Câu 3 (1đ): Xác định miền nghiệm của bất phương trình sau:
2 3 1 0. x y
Phần 2: Hình học
Câu 1 (2đ): Cho tam giác ABC biết
A B và C 1; 4 , 3; 1 6; 2 .
a) Lập phương trình tham số đường thẳng chứa cạnh BC của tam giác.
b) Lập phương trình tổng quát đường cao hạ từ A của tam giác ABC.
c) Lập phương trình tổng quát đường thẳng đi qua B và song song với đường thẳng
d x y : 3 1 0.
Câu 2 (1đ): Xét vị trí tương đối và tìm giao điểm (nếu có) của 2 đường thẳng sau:
1
d : 2 3 0 x y
và
2
d : 2 3 0.
Tìm phương trình chính tắc của Elip có một đường chuẩn là x+ 4= 0 và một tiêu điểm là điểm (-1; 0) .
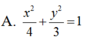
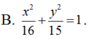
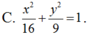
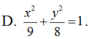
Cho hai đường thẳng d: (m – 2)x +(m – 6)y + m – 1= 0, ∆: (m – 4)x + (2m – 3)y – m + 5 = 0. Tất cả giá trị của m để hai đường thẳng cắt nhau là
A.m ≠ 3
B.m ≠ 6
C.m ≠ 3 và m ≠ - 6
D.không có m thỏa mãn
1. Phương trình tiếp tuyến d của đường tròn (C): \(x^2+y^2-3x-y=0\) tại điểm N(1;-1) là:
A. \(d:x+3y-2=0\) B. \(d:x-3y+4=0\)
C. \(d:x-3y-4=0\) D. \(d:x+3y+2=0\)
2. Cho đường tròn (C): \(x^2+y^2-4x+4y-4=0\) và điểm M(1;0). Dây cung của (C) đi qua điểm M có độ dài ngắn nhất bằng:
A. \(2\sqrt{3}\) B. \(\sqrt{5}\) C. 12 D. \(2\sqrt{7}\)
3. Lập phương trình chính tắc của parabol (P) biết (P) đi qua điểm M có hoành độ \(x_M=2\) và khoảng từ M đến tiêu điểm là \(\dfrac{5}{2}\)
A. \(y^2=8x\) B. \(y^2=4x\) C. \(y^2=x\) D. \(y^2=2x\)
C1: Trên hệ trục tọa độ Oxy, có bao nhiêu giá trị nguyên của m e [-10;10] để phương trình 2 + y ^ 2 - 2(m + 1) x + 4y + 7m + 5 = 0 là phương trình đường tròn? A.11 B.16 C.15 D.12 Câu 11 Phương trình √ x^2 -2x+4=4-x có một nghiệm là A.x=2 B.x=4 C.x=3 D. X=4
Trong mặt phẳng Oxy, hãy vẽ các đường thẳng có phương trình sau đây:
d1: x – 2y = 0;
d2: x = 2;
d3: y + 1 = 0;
d4: x/8 + y/4 = 1.