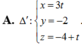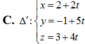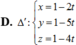Đường thẳng ∆ đi qua điểm M(3;1;1), nằm trong mặt phẳng α : x + y - z - 3 = 0 và tạo với đường thẳng d : x = 1 y = 4 + 3 t z = - 3 - 2 t một góc nhỏ nhất thì phương trình của ∆ là:
A. x = 1 y = - t ' z = 2 t '
B. x = 8 + 5 t ' y = - 3 - 4 t ' z = 2 + t '
C. x = 1 + 2 t ' y = 1 - t ' z = 3 - 2 t '
D. x = 1 + 5 t ' y = 1 - 4 t ' z = 3 + 2 t '
Dễ dàng kiểm tra được
M
∈
α
.
Gọi d ' là đường thẳng qua M và song song d. Khi đó: d ∆ = d ' ∆
Để d ∆ min thì ∆ là hình chiếu vuông góc của d ' lên α .
Phương trình đường thẳng d ' là: x = 3 y = 1 + 3 t z = 1 - 2 t
Lấy A 3 ; 4 ; - 1 ∈ d ' và A ∉ M . Tìm H là hình chiếu của A lên mặt phẳng α
Đường thẳng AH nhận n α → 1 , 1 , - 1 là 1 VTPT, có phương trình là x = 3 + t y = 4 + t z = - 1 - t
Giả sử
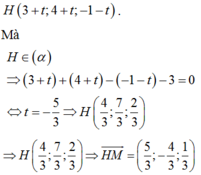
Đường thẳng ∆ đi qua M(3,1,1) và có 1 VTCP 5 ; - 4 ; 1 có PTTS là:
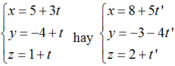
Chọn B.