Question

Dựng hình thang ABCD (AB // CD), biết AB = AD = 2cm, AC = DC = 4cm.

Answer 1

a) Phân tích :

Giả sử dựng được hình thang ABCD thỏa mãn yêu cầu đề bài.

Tam giác ADC dựng được vì biết ba cạnh của tam giác.

Điểm B phải thỏa mãn hai điều kiện :

+ B nằm trên tia Ax song song với CD

+ B cách A một đoạn 2cm.

b) Cách dựng:

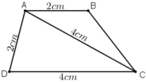
+ Dựng tam giác ADC có AD = 2cm, AC = 4cm, CD = 4cm.

+ Dựng tia Ax song song với CD và nằm trên cùng một nửa mặt phẳng chứa điểm C bờ là đường thẳng AD.

+ Trên tia Ax lấy điểm B sao cho AB = 2cm.

Kẻ BC ta được hình thang ABCD cần dựng.

c) Chứng minh

Tứ giác ABCD là hình thang vì AB // CD.

Hình thang ABCD có AB = AD = 2cm, AC = BC = 4cm thỏa mãn yêu cầu đề bài

d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn yêu cầu của đề bài.