f ' x = 3 x 2 - 18 x + 24 f ' x = 0 ⇔ x = 2 x = 4
Lập bảng biến thiên và suy ra x 1 ; y 1 = 4 ; 20 ; x 2 ; y 2 = 2 ; 24 .
Suy ra x 1 y 2 - x 2 y 1 = 56
Đáp án B
f ' x = 3 x 2 - 18 x + 24 f ' x = 0 ⇔ x = 2 x = 4
Lập bảng biến thiên và suy ra x 1 ; y 1 = 4 ; 20 ; x 2 ; y 2 = 2 ; 24 .
Suy ra x 1 y 2 - x 2 y 1 = 56
Đáp án B
Cho hàm số y = f(x) xác định trên D = − 1 ; + ∞ \ 1 . Dưới đây là một phần đồ thị của y = f(x)
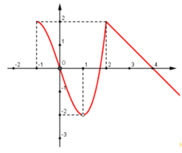
Hỏi trong các mệnh đề sau, có bao nhiêu mệnh đề đúng:
(I) Số điểm cực đại của hàm số trên tập xác định là 1.
(II) Hàm số có cực tiểu là -2 tại x = 1
(III) Hàm số đạt cực đại tại x = 2
(IV) Hàm số đạt cực đại tại x = -1
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: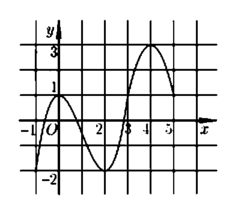
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số y = f ( x ) = x 3 + a x 2 + b x + c đạt cực tiểu bằng – 3 tại điểm x=1 và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính đạo hàm cấp một của hàm số tại x= -3
A. f'(-3)= 0
B. f'(-3)= 2
C. f'(-3)= 1
D. f'(-3)= -2
Cho hàm số y = - x 3 + 3 x 2 + 3 ( m 2 - 1 ) x - 3 m 2 - 1 . Có bao nhiêu giá trị nguyên của m để đồ thị hàm số có điểm cực đại và điểm cực tiểu nằm bên trái đường thẳng x=2
A. 3
B. 1
C. 2
D. 0
Cho hàm số y=f(x) có đồ thị đạo hàm y=f’(x) được cho như hình vẽ bên và các mệnh đề sau:
(1). Hàm số y=f(x) có duy nhất 1 điểm cực trị
(2). Hàm số y=f(x) nghịch biến trên khoảng (-2;1)
(3). Hàm số y=f(x) đồng biến trên khoảng 0 ; + ∞
(4). Hàm số g x = f x + x 2 có 2 điểm cực trị.
Số mệnh đề đúng là
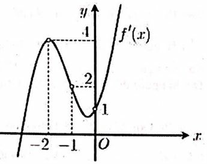
A. 1
B. 3
C. 4
D. 2
Cho hàm số y=f(x) xác định và liên tục trên R, có đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Hàm số g(x)=f(x) – 1/2 x2+ x-8 có bao nhiêu điểm cực tiểu?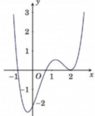
A. 3
B. 2
C. 1.
D. 4
Cho hàm số y =f(x) có đạo hàm f’(x) trên khoảng (-∞;+∞). Đồ thị của hàm số y =f(x) như hình vẽ. Đồ thị của hàm số y = f x 2 có bao nhiêu điểm cực đại, điểm cực tiểu?
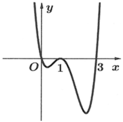
A. 1 điểm cực đại, 3 điểm cực tiểu.
B. 2 điểm cực đại, 3 điểm cực tiểu.
C. 2 điểm cực đại, 2 điểm cực tiểu.
D. 2 điểm cực tiểu, 3 điểm cực đại.
Cho hàm số y = f(x) có bảng biến thiên như sau:
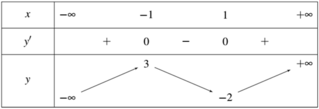
(I): Tập xác định của f(x): R \ {1}
(II): Hàm số f(x) có đúng 1 điểm cực trị
(III): min f(x) = -2
(IV): A(-1; 3) là điểm cực đại của đồ thị hàm số
Trong các phát biểu trên, có bao nhiêu phát biểu đúng?
A. 2
B. 3
C. 1
D. 0
Cho hàm số y=f(x) liên tục trên R, có đạo hàm f ’ ( x ) = x ( x – 1 ) 2 ( x + 1 ) 3 . Đồ thị hàm số y=f(x) có bao nhiêu điểm cực trị?
A. Đồ thị hàm số f(x) không có điểm cực trị
B. Đồ thị hàm số f(x) có 1 điểm cực trị
C. Đồ thị hàm số f(x) có 2 điểm cực trị
D. Đồ thị hàm số f(x) có 3 điểm cực trị