Chọn D.
Điểm O là trung điểm của đoạn AB khi và chỉ khi OA= OB và 
là ngược hướng.
Vậy 
.
Đúng 0
Bình luận (0)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn AB? A. OA OB B.
O
A
→
O
B
→
C.
A
O
→
B
O
→
D.
O...
Đọc tiếp
Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn AB?
A. OA = OB
B. O A → = O B →
C. A O → = B O →
D. O A → + O B → = 0 →
Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn thẳng AB? A. OA OB B.
O
A
→
O
B
→
C.
A
O
→
B
O
→
D. ...
Đọc tiếp
Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn thẳng AB?
A. OA = OB
B. O A → = O B →
C. A O → = B O →
D. O A → = - O B →
Cho bốn điểm phân biệt A, B, C, D. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để
A
B
→
C
D
→
? A. ABCD là hình bình hành. B. ABDC là hình bình hành. C. AC BD D. AB CD
Đọc tiếp
Cho bốn điểm phân biệt A, B, C, D. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để A B → = C D → ?
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AC = BD
D. AB = CD
Xét các phát biểu sau: (1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
B
A
→
-
2
A
C
→
(2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
C
B
→
C...
Đọc tiếp
Xét các phát biểu sau:
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là B A → = - 2 A C →
(2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là C B → = C A →
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là P Q → = 2 P M →
Trong các câu trên, thì:
A. Câu (1) và câu (3) là đúng.
B. Câu (1) là sai.
C. Chỉ có câu (3) sai.
D. Không có câu nào sai.
Cho ba điểm O, A, B thẳng hàng và biết OA = a, OB = b. Tính tích vô hướng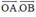 
trong hai trường hợp:
a) Điểm O nằm ngoài đoạn AB;
b) Điểm O nằm trong đoạn AB.
Cho tứ giác ABCD, I và J là trung điểm của AB và CD,O là trung điểm I. M là điểm bất kỳ.Chứng minh: a) vecto OA + vecto OB + vecto OC + vecto OD = vecto O b) vecto MA + vecto MB + vecto MC + vecto MD = 4MO c) vecto AC + vecto BD = vecto 2IJ
cho tứ giác ABCD,gọi I,J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ .chứng minh rằng: a)AC + BD 2IJ b) OA +OB +OC + OD 0 c) MA + MB +MC +MD4MO giúp em với ạ
Đọc tiếp
cho tứ giác ABCD,gọi I,J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ .chứng minh rằng: a)AC + BD =2IJ b) OA +OB +OC + OD= 0 c) MA + MB +MC +MD=4MO giúp em với ạ
Cho ba điểm A, B, C phân biệt. Điều kiện cần và đủ để ba điểm A, B, C thẳng hàng và A nằm giữa B, C là: A.
∃
k
0
:
A
B
→
k
A
C
→
B.
∃
k
≠
0
:
A...
Đọc tiếp
Cho ba điểm A, B, C phân biệt. Điều kiện cần và đủ để ba điểm A, B, C thẳng hàng và A nằm giữa B, C là:
A. ∃ k < 0 : A B → = k A C →
B. ∃ k ≠ 0 : A B → = k A C →
C. AB = AC
D. A B → = A C →
Điều kiện nào sau đây không là điều kiện cần và đủ để G là trọng tâm của tam giác ABC, với M là trung điểm của BC? A.
A
M
→
-
3
2
G
A
→
B.
2
G
M
→
G...
Đọc tiếp
Điều kiện nào sau đây không là điều kiện cần và đủ để G là trọng tâm của tam giác ABC, với M là trung điểm của BC?
A. A M → = - 3 2 G A →
B. 2 G M → = G A →
C. A G → + B G → + C G → = 0 →
D. G A → + G B → + G C → = 0 →