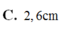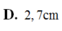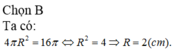Các câu hỏi tương tự
Cho mặt cầu (S) có bán kính R 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8
π
(cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu? A. 32
3
(
c
m
3
) B. 60
3...
Đọc tiếp
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Cho một khối trụ có chiều cao bằng 8 cm, bán kính đường tròn đáy bằng 6 cm. Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 4 cm. Diện tích của thiết diện được tạo thành là?
Cắt một mặt cầu (S) bởi một mặt phẳng qua tâm được thiết diện là hình tròn có đường kính bằng 4 cm. Tính thể tích của khối cầu.
Đọc tiếp
Cắt một mặt cầu (S) bởi một mặt phẳng qua tâm được thiết diện là hình tròn có đường kính bằng 4 cm. Tính thể tích của khối cầu.
![]()
![]()
![]()
![]()
Người ta tích điện một vật dẫn điện S1, hình cầu, bán kính a = 5 cm bằng một nguồn điện thế V0 = 18000 (V), xong rồi cô lập S1 và bao quanh nó bằng một vật dẫn điện rỗng S2 hình cầu, đồng tâm với S1 bán kính trong b = 6 cm, bán kính ngoài c = 8 cm. Tính điện thế V của hình cầu S1 trong các trường hợp: a) S2 trung hòa và cô lập b) S2 nối vào nguồn điện thế 5000 (V)
Cho khối cầu tâm O bán kính 6 cm. Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng: A. 2 cm. B. 3 cm. C. 4 cm. D. 0 cm.
Đọc tiếp
Cho khối cầu tâm O bán kính 6 cm. Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng:
A. 2 cm.
B. 3 cm.
C. 4 cm.
D. 0 cm.
Cho mặt cầu (S) bán kính R5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
π
(cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD.
Đọc tiếp
Cho mặt cầu (S) bán kính R=5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD.
![]()
![]()
![]()
![]()
Cho khối nón tròn xoay có đường cao h 20 cm, bán kính đáy r 25 cm. Một mặt phẳng (P) chứa đỉnh S và giao tuyến với mặt phẳng đáy là AB. Khoảng cách từ tâm O của đáy đến mặt phẳng (P) là 12 cm. Khi đó diện tích thiết diện của (P) với khối nón bằng: A. 500
c
m
2
B. 475
c
m
2
C. 450
c
m
2
D. 550...
Đọc tiếp
Cho khối nón tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm. Một mặt phẳng (P) chứa đỉnh S và giao tuyến với mặt phẳng đáy là AB. Khoảng cách từ tâm O của đáy đến mặt phẳng (P) là 12 cm. Khi đó diện tích thiết diện của (P) với khối nón bằng:
A. 500 c m 2
B. 475 c m 2
C. 450 c m 2
D. 550 c m 2
Một chậu nước hình bán cầu bằng nhôm có bán kính R10(cm). Trong chậu có chứa sẵn mọt khối nước hình chõm cầu có chiều cao h4(cm). Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi. Tính bán kinh của viên bi (kết quả làm tròn đến 2 chữ số lẻ thập phân).
Đọc tiếp
Một chậu nước hình bán cầu bằng nhôm có bán kính R=10(cm). Trong chậu có chứa sẵn mọt khối nước hình chõm cầu có chiều cao h=4(cm). Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi. Tính bán kinh của viên bi (kết quả làm tròn đến 2 chữ số lẻ thập phân).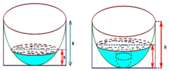
![]()
![]()
![]()
![]()
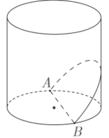
Cho khối trụ có bán kính đáy bằng 4(cm) và chiều cao 5(cm). Gọi AB là một dây cung đáy dưới sao cho AB
4
3
(cm). Người ta dựng mặt phẳng (P) đi qua hai điểm A, B và tạo với mặt phẳng đáy hình trụ một góc
60
°
như hình vẽ. Tính diện tích thiết diện của hình trụ cắt bởi mặt phẳng (P).
Đọc tiếp
Cho khối trụ có bán kính đáy bằng 4(cm) và chiều cao 5(cm). Gọi AB là một dây cung đáy dưới sao cho AB= 4 3 (cm). Người ta dựng mặt phẳng (P) đi qua hai điểm A, B và tạo với mặt phẳng đáy hình trụ một góc 60 ° như hình vẽ. Tính diện tích thiết diện của hình trụ cắt bởi mặt phẳng (P).
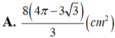
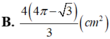
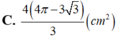
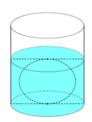
Người ta thả một viên billiards snooker có dạng hình cầu với bán kính nhỏ hơn 4,5 cm vào một chiếc cốc hình trụ đang chứa nước thì viên billiards đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4 cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5 cm. Bán kính của viên billiards đó bằng
Đọc tiếp
Người ta thả một viên billiards snooker có dạng hình cầu với bán kính nhỏ hơn 4,5 cm vào một chiếc cốc hình trụ đang chứa nước thì viên billiards đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4 cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5 cm. Bán kính của viên billiards đó bằng
![]()
![]()