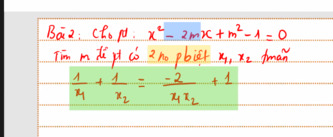
Ta có: \(\Delta'=\left(-m\right)^2-\left(m^2-1\right)=m^2-m^2+1=1>0\)
\(\Rightarrow\) pt 2 luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2-1\end{matrix}\right.\)
\(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{-2}{x_1x_2}+1\\ \Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}=\dfrac{-2}{2m}+1\left(m\ne0\right)\\ \Leftrightarrow\dfrac{m^2-1}{2m}+\dfrac{1}{m}-1=0\\ \Leftrightarrow\dfrac{m^2-1}{2m}+\dfrac{2}{2m}-\dfrac{2m}{2m}=0\\ \Leftrightarrow\dfrac{m^2-1+2-2m}{2m}=0\\ \Rightarrow m^2-2m+1=0\\ \Leftrightarrow\left(m-1\right)^2=0\\ \Leftrightarrow m-1=0\\ \Leftrightarrow m=1\)