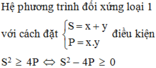Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Cho phương trìnhleft(m-1right)x^2-2left(m-3right)x+m+100m khác 1a/ xác định mm để phương trình có 2 nghiệm x1. x2b/ Tìm m để phương trình có nghiệm x10, khi đó tìm nghiệm còn lạic/ Với điều kiện của m vừa tìm được ở câu a, tìm hệ thức liên hệ giữa x1, x2 độc lập đối với tham số md/ Với đièu kiện của mm vừa tìm được ở câu a, gọi S và P lần lượt là tông và tích của 2 nghiệm của phương trình. Tìm các giá trị của m để S và P là các số nguyên
Đọc tiếp
Cho phương trình
\(\left(m-1\right)x^2-2\left(m-3\right)x+m+1=0\)0
m khác 1
a/ xác định mm để phương trình có 2 nghiệm x1. x2
b/ Tìm m để phương trình có nghiệm x1=0, khi đó tìm nghiệm còn lại
c/ Với điều kiện của m vừa tìm được ở câu a, tìm hệ thức liên hệ giữa x1, x2 độc lập đối với tham số m
d/ Với đièu kiện của mm vừa tìm được ở câu a, gọi S và P lần lượt là tông và tích của 2 nghiệm của phương trình. Tìm các giá trị của m để S và P là các số nguyên
cho hệ phương trình \(\hept{\begin{cases}\text{x+my=2}\\\text{mx-y=1}\end{cases}}\)
a) tìm số nguyên m để hệ có nghiệm (x;y) thỏa mãn x>0 và y<0
b) tìm giá trị lớn nhất của biểu thức S = 2x-y với (x;y) là nghiệm của hệ phương trình đã cho.
CHo phương trình
\(\left(m-1\right)x^2-2\left(m-3\right)x+m+1=0\)0
với điều kiện của m để pt có nghiêm, gọi S và P lần lượt là tổng và tích của 2 nghiệm pt. Tìm các giá trị của m để S và P là các số nguyên
Cho phương trình
\(\left(m-1\right)x^2-2\left(m-3\right)x+m+1\)1=0
Với điều kiện của m để phương trình có 2 nghiệm x1, x2, gọi S và P lần lượt là tổng và tích của 2 nghiệm của phương trình. Tìm các giá trị của m để S và P là các số nguyên
Cho phương trình \(\left(m-1\right)x^2-2\left(m-3\right)x+m+1=0\)0
với m khác 1
Với điều kiện của m vừa tìm được ở câu a, gọi S và P lần lượt là tổng và tích của 2 nghiệm của phương trình. Tìmm các giá trị của m để S và P là các số nguyên
cho a, b là các số thực thỏa mãn điều kiện a^2 + b^2 = 4 + ab Chứng minh rằng 8/3 ≤ a^2 + b^2 ≤ 8
Dấu bằng xảy ra khi nào?
b. Cho (x,y) là nghiệm của phuơng trình x^2 + 3y^2 + 2xy - 10x - 14y+18 =0. Tìm nghiệm (x,y ) sao cho S = x + y đạt giá trị lớn nhất và nhỏ nhất .
Cho a, b là các số thực thỏa mãn điều kiện a^2 + b^2 = 4 + ab Chứng minh rằng 8/3 ≤ a^2 + b^2 ≤ 8
Dấu bằng xảy ra khi nào?
b. Cho (x,y) là nghiệm của phuơng trình x^2 + 3y^2 + 2xy - 10x - 14y+18 =0. Tìm nghiệm (x,y ) sao cho S = x + y đạt giá trị lớn nhất và nhỏ nhất .
Hệ phương trình
(m+1)x-y=m+1x+(m-1)y=2có nghiệm là x0;y0
Giá trị nhỏ nhất S= x0+y0
bài 1 : Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình :a) 5 + 2x – 4 0 ; b) 4 – 6x + 4 0 ;bài 2 :Dùng hệ thức Vi-ét để tính nhẩm nghiệm của phương trình :a) 7 + 3x – 4 0 ;b) 4 – (5 + ) x + 1 + 0.
Đọc tiếp
bài 1 : Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình :
a) 5 + 2x – 4 = 0 ;
b) 4 – 6
x + 4 = 0 ;
bài 2 :
Dùng hệ thức Vi-ét để tính nhẩm nghiệm của phương trình :
a) 7 + 3x – 4 = 0 ;
b) 4 – (5 +
) x + 1 +
= 0.
cho hệ phương trình
\(\hept{\begin{cases}\left(m+1\right)x-y=m+1\\x+\left(m-1\right)y=2\end{cases}}\)
TÌm m để hệ phương trình có nghiệm duy nhất (x0,y0) sao cho S =x0 +y0 đạt GTLN