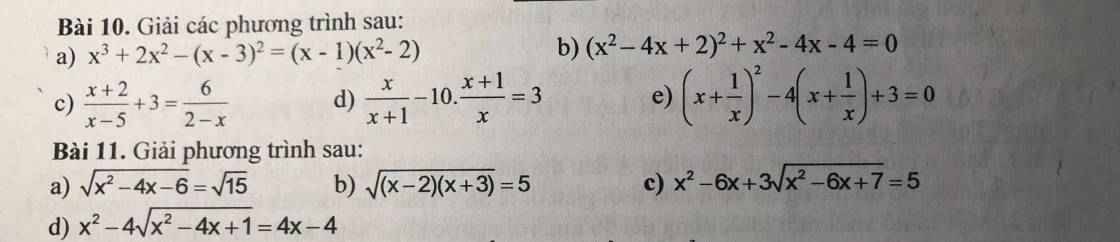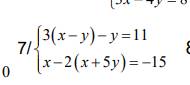10a/
$x^3+2x^2-(x-3)^2=(x-1)(x^2-2)$
$\Leftrightarrow x^3+2x^2-(x^2-6x+9)=x^3-x^2-2x+2$
$\Leftrightarrow x^3+x^2+6x-9=x^3-x^2-2x+2$
$\Leftrightarrow 2x^2+8x-11=0$
$\Leftrightarrow x^2+4x-5,5=0$
$\Leftrightarrow (x^2+4x+4)-9,5=0$
$\Leftrightarrow (x+2)^2=9,5$
$\Leftrightarrow x+2=\pm \sqrt{9,5}$
$\Leftrightarrow x=-2\pm \sqrt{9,5}$
10b/
$(x^2-4x+2)^2+x^2-4x-4=0$
$\Leftrightarrow (x^2-4x+2)^2+(x^2-4x+2)-6=0$
$\Leftrightarrow a^2+a-6=0$ (đặt $x^2-4x+2=a$)
$\Leftrightarrow (a^2-2a)+(3a-6)=0$
$\Leftrightarrow a(a-2)+3(a-2)=0$
$\Leftrightarrow (a-2)(a+3)=0$
$\Leftrightarrow (x^2-4x+2-2)(x^2-4x+2+3)=0$
$\Leftrightarrow (x^2-4x)(x^2-4x+5)=0$
$\Leftrightarrow x(x-4)(x^2-4x+5)=0$
\(\Leftrightarrow \left[\begin{matrix} x=0\\ x-4=0\\ x^2-4x+5=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=0(\text{chọn})\\ x=4(\text{chọn})\\ (x-2)^2=-1<0(\text{loại})\end{matrix}\right.\)
10c/
ĐKXĐ: $x\neq 5; x\neq 2$
\(PT \Leftrightarrow \frac{x+2+3(x-5)}{x-5}=\frac{6}{2-x}\\ \Leftrightarrow \frac{4x-13}{x-5}=\frac{6}{2-x}\\ \Rightarrow (4x-13)(2-x)=6(x-5)\\ \Leftrightarrow -4x^2+21x-26=6x-30\\ \Leftrightarrow -4x^2+15x+4=0\\ \Leftrightarrow 4x^2-15x-4=0\\ \Leftrightarrow (x-4)(4x+1)=0\\ \Leftrightarrow \left[\begin{matrix} x-4=0\\ 4x+1=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=4\\ x=\frac{-1}{4}\end{matrix}\right.\)
10d/
ĐKXĐ: $x\neq 0; x\neq -1$
\(PT \Leftrightarrow \frac{x}{x+1}-10(1+\frac{1}{x})=3\\ \Leftrightarrow \frac{x}{x+1}-\frac{10}{x}=13\\ \Leftrightarrow \frac{x^2-10x-10}{x(x+1)}=13\\ \Rightarrow x^2-10x-10=13x(x+1)\\ \Leftrightarrow 12x^2+23x+10=0\\ \Leftrightarrow (3x+2)(4x+5)=0\\ \Leftrightarrow \left[\begin{matrix} 3x+2=0\\ 4x+5=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{-2}{3}\\ x=\frac{-5}{4}\end{matrix}\right.\)
10e/
ĐKXĐ: $x\neq 0$
Đặt $x+\frac{1}{x}=a$ thì PT trở thành:
$a^2-4a+3=0$
$\Leftrightarrow (a^2-a)-(3a-3)=0$
$\Leftrightarrow a(a-1)-3(a-1)=0$
$\Leftrightarrow (a-1)(a-3)=0$
$\Leftrightarrow (x+\frac{1}{x}-1)(x+\frac{1}{x}-3)=0$
$\Leftrightarrow \frac{x^2-x+1}{x}.\frac{x^2-3x+1}{x}=0$
$\Rightarrow (x^2-x+1)(x^2-3x+1)=0$
$\Leftrightarrow x^2-x+1=0$ hoặc $x^2-3x+1=0$
Nếu $x^2-x+1=0$
$\Leftrightarrow (x-\frac{1}{2})^2=\frac{-3}{4}<0$ (vô lý - loại)
Nếu $x^2-3x+1=0$
$\Leftrightarrow (x-1,5)^2=1,25$
$\Leftrightarrow x-1,5=\pm \sqrt{1,25}$
$\Leftrightarrow x=1,5\pm \sqrt{1,25}$ (tm)
11a/ ĐKXĐ:.........
PT $\Leftrightarrow x^2-4x-6=15$ (bình phương hai vế)
$\Leftrightarrow x^2-4x-21=0$
$\Leftrightarrow (x^2+3x)-(7x+21)=0$
$\Leftrightarrow x(x+3)-7(x+3)=0$
$\Leftrightarrow (x+3)(x-7)=0$
$\Leftrightarrow x+3=0$ hoặc $x-7=0$
$\Leftrightarrow x=-3$ hoặc $x=7$ (đều thỏa mãn)
b. ĐKXĐ:...........
PT $\Leftrightarrow (x-2)(x+3)=5^2=25$
$\Leftrightarrow x^2+x-6=25$
$\Leftrightarrow x^2+x-31=0$
$\Leftrightarrow (x+\frac{1}{2})^2=\frac{125}{4}$
$\Leftrightarrow x+\frac{1}{2}=\pm \frac{5\sqrt{5}}{2}$
$\Leftrightarrow x=\frac{-1\pm 5\sqrt{5}}{2}$ (đều tm)
10c/ ĐKXĐ:.........
PT $\Leftrightarrow (x^2-6x+7)+3\sqrt{x^2-6x+7}=12$
$\Leftrightarrow a^2+3a=12$ (đặt $\sqrt{x^2-6x+7}=a$, $a\geq 0$)
$\Leftrightarrow a^2+3a-12=0$
$\Leftrightarrow (a+\frac{3}{2})^2=\frac{57}{4}$
$\Leftrightarrow a=\frac{-3\pm \sqrt{57}}{2}$
Do $a\geq 0$ nên $a=\frac{-3+\sqrt{57}}{2}$
$\Leftrightarrow \sqrt{x^2-6x+7}=\frac{-3+\sqrt{57}}{2}$
$\Leftrightarrow x^2-6x+7=(\frac{-3+\sqrt{57}}{2})^2=\frac{33-3\sqrt{57}}{2}$
$\Leftrightarrow x^2-6x+9=\frac{37-3\sqrt{57}}{2}$
$\Leftrightarrow (x-3)^2=\frac{37-3\sqrt{57}}{2}$
$\Leftrightarrow x=3\pm \sqrt{\frac{37-3\sqrt{57}}{2}}$
10d/ ĐKXĐ:..........
PT $\Leftrightarrow (x^2-4x+1)-4\sqrt{x^2-4x+1}+3=0$
$\Leftrightarrow a^2-4a+3=0$ (đặt $\sqrt{x^2-4x+1}=a$, $a\geq 0$)
$\Leftrightarrow (a-1)(a-3)=0$
$\Leftrightarrow a=1$ hoặc $a=3$
TH $a=1$
$\Leftrightarrow \sqrt{x^2-4x+1}=1$
$\Leftrightarrow x^2-4x=0$
$\Leftrightarrow x(x-4)=0$
$\Leftrightarrow x=0$ hoặc $x-4=0$
$\Leftrightarrow x=0$ hoặc $x=4$ (tm)
TH $a=3$
$\Leftrightarrow \sqrt{x^2-4x+1}=3$
$\Leftrightarrow x^2-4x+1=9$
$\Leftrightarrow x^2-4x+4=12$
$\Leftrightarrow (x-2)^2=12$
$\Leftrightarrow x=2\pm \sqrt{12}$
Vậy...........