Các câu hỏi tương tự
Có thể chia một hình lập phương thành bao nhiêu tứ diện bằng nhau
A. Hai B. Vô số
C. Bốn D. Sáu.
Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương? A. 2 B. 8 C. 4 D. 6
Đọc tiếp
Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương?
A. 2
B. 8
C. 4
D. 6
Chia khối lập phương thành sáu khối tứ diện bằng nhau.
Cho tứ diện ABCD có AD ⊥ (ABC) và BD ⊥ BC. Khi quay tứ diện đó xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
A. Một B. Hai
C. Ba D. Bốn
Người ta cắt đôi đoạn dây thép dài 10m thành hai phần. Phần 1 lại cắt thành 6 phần bằng nhau và ghép thành một hình tứ diện, phần 2 lại cắt thành 12 phần bằng nhau và ghép thành một hình lập phương sao cho tổng diện tích xung quanh của hai hình là nhỏ nhấtGọi a là độ dài cạnh của hình tứ diện, b là độ dài cạnh của hình lập phương thì a+b là: A.
5
+
5
3
3
B. ...
Đọc tiếp
Người ta cắt đôi đoạn dây thép dài 10m thành hai phần. Phần 1 lại cắt thành 6 phần bằng nhau và ghép thành một hình tứ diện, phần 2 lại cắt thành 12 phần bằng nhau và ghép thành một hình lập phương sao cho tổng diện tích xung quanh của hai hình là nhỏ nhất

Gọi a là độ dài cạnh của hình tứ diện, b là độ dài cạnh của hình lập phương thì a+b là:
A. 5 + 5 3 3
B. - 5 + 5 3 3
C. - 5 + 20 3 6
D. 5 + 20 3 6
Cho tứ diện đều ABCD. Khi quay tứ diện đó xung quanh trục là AB có bao nhiêu hình nón khác nhau được tạo thành?
A. Một B. Hai
C. Ba D. Không có hình nón nào
Cho khối tứ diện ABCD. Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D. Bằng hai mặt phẳng (CDM) và (ABN), ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây? A. MANC, BCDN, AMND, ABND B. MANC, BCMN, AMND, MBND C. ABCN, ABND, AMND, MBND D. NACB, BCMN, ABND, MBND
Đọc tiếp
Cho khối tứ diện ABCD. Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D. Bằng hai mặt phẳng (CDM) và (ABN), ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây?
A. MANC, BCDN, AMND, ABND
B. MANC, BCMN, AMND, MBND
C. ABCN, ABND, AMND, MBND
D. NACB, BCMN, ABND, MBND
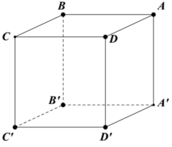
Cho hình lập phương ABCDA'B'C'D'. Có bao nhiêu mặt trụ tròn xoay đi qua sáu đỉnh A, B, D, C', B', D'?
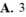
![]()
![]()
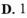
Cho hình lập phương ABCD.A'B'C'D'. Có bao nhiêu mặt trụ tròn xoay đi qua sáu đỉnh A, B, D, C', B', D' ?
A. 3
B. 2
C.1
D. 4

