Đáp án B.
Với 4 y - y - 1 + y + 3 2 ≤ 8
xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm - 3 ≤ y ≤ 0
Khi đó 3 x 2 - 2 x - 3 - log 3 5 = 3 x 2 - 2 x - 3 3 log 3 5 = 3 x 2 - 2 x - 3 5 ≥ 1 5
và y ∈ - 3 ; 0 ⇔ y + 4 ∈ 1 ; 4 ⇒ 5 - y + 4 ≤ 5 - 1 = 1 5
Do đó
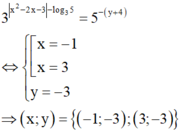
Vậy có tất cả hai cặp số thực (x; y) thỏa mãn yêu cầu bài toán.

