Các câu hỏi tương tự
Cho các phát biểu sau, số phát biểu đúng: 1. Có một và chỉ một đường thẳng đi qua 2 điểm phân biệt 2. Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt 3. Nếu 1 đường thẳng có 1 điểm thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó 4. Tồn tại 4 điểm không cùng thuộc một mặt phẳng 5. Tồn tại 4 điểm cùng thuộc một mặt phẳng 6. Nếu 2 mặt phẳng phân biệt có 1 điểm chung thì chúng sẽ còn 1 điểm chung khác 7. Trên mỗi mặt phẳng, các kết quả đã biết tr...
Đọc tiếp
Cho các phát biểu sau, số phát biểu đúng:
1. Có một và chỉ một đường thẳng đi qua 2 điểm phân biệt
2. Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt
3. Nếu 1 đường thẳng có 1 điểm thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó
4. Tồn tại 4 điểm không cùng thuộc một mặt phẳng
5. Tồn tại 4 điểm cùng thuộc một mặt phẳng
6. Nếu 2 mặt phẳng phân biệt có 1 điểm chung thì chúng sẽ còn 1 điểm chung khác
7. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng có thể không đúng
A. 3
B. 4
C. 5
D. 6
Cho bốn điểm A,B,C,D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại I. Điểm I không thuộc mặt phẳng nào sau đây: A. (ACD) B. (CMN) C. (BCD) D. (ABD)
Đọc tiếp
Cho bốn điểm A,B,C,D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại I. Điểm I không thuộc mặt phẳng nào sau đây:
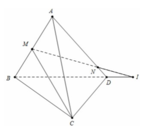
A. (ACD)
B. (CMN)
C. (BCD)
D. (ABD)
Số phát biểu đúng 1. Trong không gian qua 1 điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho 2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy đồng quy 3. Nếu 2 mặt phẳng phân biệt lần lượt chứa 2 đường thẳng song song thì giao tuyến của chúng ( nếu có ) cũng song song với 2 đường thẳng đó hoặc trùng với một trong 2 đường thẳng đó 4. 2 đường thẳng phân biệt cùng song song với đường thẳng th...
Đọc tiếp
Số phát biểu đúng
1. Trong không gian qua 1 điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy đồng quy
3. Nếu 2 mặt phẳng phân biệt lần lượt chứa 2 đường thẳng song song thì giao tuyến của chúng ( nếu có ) cũng song song với 2 đường thẳng đó hoặc trùng với một trong 2 đường thẳng đó
4. 2 đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì chúng song song với nhau
5. Nếu đường thẳng d không nằm trong mặt phẳng ( ) và d song song với đường thẳng d’ nằm trong ( ) thì d song song với ( )
6. Cho đường thẳng a song song với mặt phẳng . Nếu mặt phẳng chứa a và cắt theo giao tuyến b thì b song song với a
7. Nếu 2 mặt phẳng cùng song song với 1 đường thẳng thì giao tuyến của chúng ( nếu có ) cũng song song với đường thẳng đó
8. Cho 2 đường thẳng chéo nhau. Có vô số mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
A. 8
B. 7
C. 6
D. 5
Xét các khẳng định sau đây xem khẳng định nào đúng, khẳng định nào sai?a) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.b) Qua một đường thẳng, có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.c) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.d) Cho hai đường thẳng a và b. Nếu có mặt phẳng (α) không chứa cả a và b thì a và b chéo nhau.
Đọc tiếp
Xét các khẳng định sau đây xem khẳng định nào đúng, khẳng định nào sai?
a) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
b) Qua một đường thẳng, có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
c) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
d) Cho hai đường thẳng a và b. Nếu có mặt phẳng (α) không chứa cả a và b thì a và b chéo nhau.
Trong các mệnh đề sau, những mệnh đề nào đúng?(1) Hai đường thẳng chéo nhau thì không có điểm chung.(2) Hai đường thẳng không có điểm chung thì chéo nhau.(3) Hai đường thẳng chéo nhau thì không cùng thuộc một mặt phẳng.(4) Hai đường thẳng không song song thì chéo nhau. A. (1), (3), (4) B. (1), (2), (3), (4) B. C. (2). (3), (4) D. (1), (3).
Đọc tiếp
Trong các mệnh đề sau, những mệnh đề nào đúng?
(1) Hai đường thẳng chéo nhau thì không có điểm chung.
(2) Hai đường thẳng không có điểm chung thì chéo nhau.
(3) Hai đường thẳng chéo nhau thì không cùng thuộc một mặt phẳng.
(4) Hai đường thẳng không song song thì chéo nhau.
A. (1), (3), (4)
B. (1), (2), (3), (4)
B. C. (2). (3), (4)
D. (1), (3).
Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng.a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD), (BCE) và (ADF).b) Lấy điểm M thuộc đoạn DF. Tìm giao điểm của đường thẳng AM với mặt phẳng (BCE).c) Chứng minh hai đường thẳng AC và BF không cắt nhau.
Đọc tiếp
Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng.
a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD), (BCE) và (ADF).
b) Lấy điểm M thuộc đoạn DF. Tìm giao điểm của đường thẳng AM với mặt phẳng (BCE).
c) Chứng minh hai đường thẳng AC và BF không cắt nhau.
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn. Gọi M là trung điểm của đoạn AB, E là giao điểm của hai cạnh của hình thang ABCD và G là trọng tâm của tam giác ECD.(a) Chứng minh rằng bốn điểm S, E, M, G cùng thuộc một mặt phẳng (α) và mặt phẳng này cắt cả hai mặt phẳng (SAC) và (SBD) theo cùng một giao tuyến d.(b) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).(c) Lấy một điểm K trên đoạn SE và gọi C SC ∩KB, DSD ∩KA. Chứng minh rằng hai giao điểm của AC và BD thuộc đườn...
Đọc tiếp
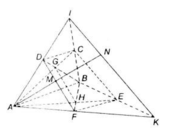
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn. Gọi M là trung điểm của đoạn AB, E là giao điểm của hai cạnh của hình thang ABCD và G là trọng tâm của tam giác ECD.
(a) Chứng minh rằng bốn điểm S, E, M, G cùng thuộc một mặt phẳng (α) và mặt phẳng này cắt cả hai mặt phẳng (SAC) và (SBD) theo cùng một giao tuyến d.
(b) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).
(c) Lấy một điểm K trên đoạn SE và gọi C' = SC ∩KB, D'=SD ∩KA. Chứng minh rằng hai giao điểm của AC' và BD' thuộc đường thẳng d nói trên.
Xét các mệnh đề sau: (I) Có một và chỉ một đường thẳng đi qua 2 điểm phân biệt. (II) Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt. (III) Nếu 2 mặt phẳng có một điểm chung thì chúng có duy nhất một điểm chung khác nữa. (IV) Nếu 1 đường thẳng có 2 điểm phân biệt thuộc mặt phẳng thì mọi điểm của đường thẳng đó đều thuộc mặt phẳng. Số mệnh đề sai là: A. 1. B. 2. C. 3. D. 4.
Đọc tiếp
Xét các mệnh đề sau:
(I) Có một và chỉ một đường thẳng đi qua 2 điểm phân biệt.
(II) Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt.
(III) Nếu 2 mặt phẳng có một điểm chung thì chúng có duy nhất một điểm chung khác nữa.
(IV) Nếu 1 đường thẳng có 2 điểm phân biệt thuộc mặt phẳng thì mọi điểm của đường thẳng đó đều thuộc mặt phẳng.
Số mệnh đề sai là:
A. 1.
B. 2.
C. 3.
D. 4.
Trên mặt phẳng cho 6 điểm phân biệt A, B, C, D, E; F. Hỏi có bao nhiêu vectơ khác vectơ – không, mà có điểm đầu và điểm cuối là các điểm đã cho ? A. 100. B. 120. C. 30. D. 25.
Đọc tiếp
Trên mặt phẳng cho 6 điểm phân biệt A, B, C, D, E; F. Hỏi có bao nhiêu vectơ khác vectơ – không, mà có điểm đầu và điểm cuối là các điểm đã cho ?
A. 100.
B. 120.
C. 30.
D. 25.

