Điều kiện xác định x∈Rx∈R.
Đặt t=√x2+1 (t≥1t≥1)
Phương trình trở thành t2−1−4t−m+1=0
⇔t2−4t=m
⇔t2−4t=m. (1)
Để phương trình có 44 nghiệm phân biệt thì phương trình (1) có hai nghiệm phân biệt lớn hơn 11.
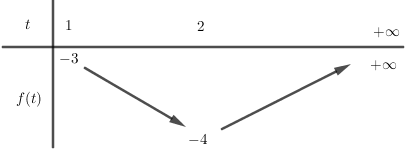
Xét hàm số f(t)=t2−4t có đồ thị là parabol có hoành độ đỉnh x=2∈(1;+∞) nên ta có bảng biến thiên:
Dựa BBT ta thấy để (1) có hai nghiệm phân biệt lớn hơn 11 thì −4<m<−3
Vậy không có giá trị nguyên của mm thỏa mãn yêu cầu bài toán.