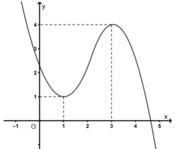
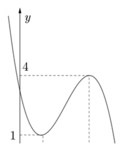
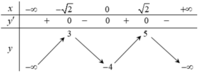
Đáp án A
PT 
Xét hàm số f t = t 3 + 3 t trên ℝ.
Ta có
f ' t = 3 t 3 + 3 > 0 ∀ t ∈ ℝ
nên hàm số f(t) đồng biến trên R
suy ra (1)
⇔ cos 3 x - 3 cos x = m
Đặt sin x=t, t ∈ - 1 ; 1 . Phương trình trở thành
t 3 - 3 t = m
Xét hàm số g ' t = t 3 - 3 t
trên t ∈ - 1 ; 1 ta có
g ' t = 3 t 2 - 3 ≤ 0 , ∀ t ∈ - 1 ; 1
và g ' t = 0 ⇔ t = ± 1
Suy ra hàm số g(t) nghịch biến trên [−1;1].
Để phương trình đã cho có nghiệm thực
⇔ t 3 - 3 t = m có nghiệm trên
Vậy có 5 giá trị nguyên của m
Cho hàm số y = a x 3 + b x 2 + c x + d ; với a, b, c, d là các số thực, có đồ thị như hình vẽ bên:
Có bao nhiêu giá trị nguyên của tham số m để phương trình f 2 x 2 = m có đúng 3 nghiệm thực phân biệt ?
A. 1
B. 2
C. 3
D. Vô số.
Cho phương trình 2 x - 1 2 . log 2 x 2 - 2 x + 3 = 4 x - m log 2 2 x - m + 2 với m là tham số thực. Có bao nhiêu giá trị nguyên của m trên đoạn - 2019 ; 2019 để phương trình có đúng 2 nghiệm phân biệt.
A. 4036
B. 4034
C. 4038
D. 4040
Cho hàm số f(x)=x^2-4x+3. Có bao nhieu giá trị nguyên của tham số m để phương trình f^2(/x/)-(m-6)f(/x/)-m+5=0 có 6 nghiệm phân biệt
Xác định giá trị của tham số m để phương trình x 3 + m x 2 + x - 5 = 0 có nghiệm dương
A. m = 5; B. m ∈ R;
C. m = -3; D. m < 0
Xác định giá trị của tham số m để phương trình x 3 + m x 2 + x - 5 = 0 có nghiệm dương
A. m = 5; B. m ∈ R;
C. m = -3; D. m < 0
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d với a, b, c, d là các số thực, có đồ thị như hình bên.
Có bao nhiêu giá trị nguyên của tham số m để phương trình f e x 2 = m có ba nghiệm phân biệt?
A. Vô số.
B. 3.
C. 1.
D. 2.
Có bao nhiêu giá trị nguyên của tham số m để phương trình 1 + x + 8 - x + 8 + 7 x - 7 x 2 = m có nghiệm thực?
A. 13.
B. 12.
C. 6.
D. 7.
Cho hàm số y = f(x) liên tục trên R và có và có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình 2 f ( sin x - cos x ) = m - 1 có hai nghiệm phân biệt trên khoảng - π 4 ; 3 π 4
A. 13.
B. 12.
C. 11.
D. 21.
Có bao nhiêu giá trị thực của tham số m để phương trình m . 3 x 2 - 3 x + 2 + 3 4 - x 2 = 3 6 - 3 x + m 1 có đúng 3 nghiệm phân biệt
A.4
B.2
C.3
D.1
Có bao nhiêu giá trị nguyên của m để phương trình \(9.3^{2x}-m\left(4.\sqrt[4]{x^2+2x+1}+3m+3\right)3^x+1=0\)có 3 nghiệm thực phân biệt
