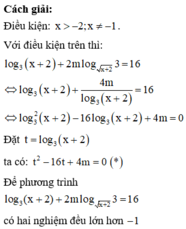Các câu hỏi tương tự
Cho phương trình
log
2
x
−
x
2
−
1
.
log
5
x
−
x
2
−
1...
Đọc tiếp
Cho phương trình log 2 x − x 2 − 1 . log 5 x − x 2 − 1 = log m x + x 2 − 1 . Có bao nhiêu giá trị nguyên dương khác 1 của m sao cho phương trình đã cho có nghiệm x lớn hơn 2?
A. Vô số
B. 3
C. 2
D. 1
Cho phương trình:
sin
3
x
+
2
sin
x
+
3
2
c
o
s
3
x
+
m
2
c
o
s
3
x...
Đọc tiếp
Cho phương trình:
sin 3 x + 2 sin x + 3 = 2 c o s 3 x + m 2 c o s 3 x + m - 2 + 2 c o s 3 x + c o s 2 x + m .
Có bao nhiêu giá trị nguyên của tham số m để phương trình trên có đúng 1 nghiệm x ∈ 0 ; 2 π 3 ?
A. 2
B. 1
C. 3
D. 4
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình
log
(
(
m
-
1
)
.
16
x
+
2
.
25
x
5...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
A. 4.
B. 3.
C. 1.
D. 2.
Có bao nhiêu giá trị nguyên của tham số m để phương trình
6
+
x
-
2
-
x
-
3
+
x
-
6
-
x
-
5
-
m
0
có nghiệm thực A. 0 B. 2 C. 3 D. 1
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6 + x - 2 - x - 3 + x - 6 - x - 5 - m = 0 có nghiệm thực
A. 0
B. 2
C. 3
D. 1
Gọi S (a;b) là tập các giá trị thực của m để phương trình
2017
2018
x
−
1
x
−
2
m
2
+
m
+
1
có hai nghiệm phân biệt đều lớn hơn 1 . Tính giá trị của...
Đọc tiếp
Gọi S = (a;b) là tập các giá trị thực của m để phương trình 2017 2018 x − 1 x − 2 = m 2 + m + 1 có hai nghiệm phân biệt đều lớn hơn 1 . Tính giá trị của T = a b .
A. T = 1 2018 .
B. T = 2017 2018 .
C. T = 1 5 .
D. T = 1 10 .
Cho hàm số
y
f
x
có đồ thị như hình vẽ . Tìm tất cả các giá trị thực của tham số m để phương trình
f
x
−
m
0
có đúng 2 nghiệm và giá trị tuyệt đối của 2 nghiệm này đều lớn hơn 1 A.
m
−
4
B.
−
4
m
−
3
C.
m...
Đọc tiếp
Cho hàm số y = f x có đồ thị như hình vẽ . Tìm tất cả các giá trị thực của tham số m để phương trình f x − m = 0 có đúng 2 nghiệm và giá trị tuyệt đối của 2 nghiệm này đều lớn hơn 1
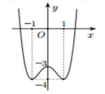
A. m > − 4
B. − 4 < m < − 3
C. m > − 3
D. − 4 < m ≤ − 3
Biết hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
đạt cực trị tại hai điểm
x
1
,
x
3
Có bao nhiêu giá trị nguyên của m để phương trình
f
x
f
m
có đúng 3 nghiệm thực phân biệt. A. 5 B. 4...
Đọc tiếp
Biết hàm số f x = a x 3 + b x 2 + c x + d đạt cực trị tại hai điểm x = 1 , x = 3 Có bao nhiêu giá trị nguyên của m để phương trình f x = f m có đúng 3 nghiệm thực phân biệt.
A. 5
B. 4
C. 7
D. 1
Có tất cả bao nhiêu số nguyên m để phương trình
log
(
m
-
x
)
3
log
(
4
-
2
x
-
3
)
có hai nghiệm thực phân biệt. A. 6. B. 2. C. 3. D. 5.
Đọc tiếp
Có tất cả bao nhiêu số nguyên m để phương trình log ( m - x ) = 3 log ( 4 - 2 x - 3 ) có hai nghiệm thực phân biệt.
A. 6.
B. 2.
C. 3.
D. 5.
Phương trình
(
m
4
+
m
+
1
)
x
2011
+
x
5
-
32
0
(1) Phương trình trên có ít nhất một nghiệm dương với mọi giá trị của m.(2) Phương trình trên vô nghiệm(3) Phương trình trên có nghiệm với mọi mChọn đáp án đúng A. Cả 3 đều sai B. Cả 3 đều đúng C. Chỉ có (1) đúng D. (1),(3) Đúng
Đọc tiếp
Phương trình ( m 4 + m + 1 ) x 2011 + x 5 - 32 = 0
(1) Phương trình trên có ít nhất một nghiệm dương với mọi giá trị của m.
(2) Phương trình trên vô nghiệm
(3) Phương trình trên có nghiệm với mọi m
Chọn đáp án đúng
A. Cả 3 đều sai
B. Cả 3 đều đúng
C. Chỉ có (1) đúng
D. (1),(3) Đúng