\(\overline{x,y}\) = \(\overline{y,x}\) \(\times\) 3 + 1,3
\(\overline{x,y}\) \(\times\) 10 = (\(\overline{y,x}\) \(\times\) 3 + 1,3)\(\times\) 10
\(\overline{xy}\) = \(\overline{yx}\) \(\times\) 3+ 13
\(x\times10\) + \(y\) = \(y\times\) 10 \(\times\) \(\)3+ \(x\) \(\times\)3 + 13
\(x\times10\) = \(y\times30\) + \(x\)\(\times\)3 + 13 - \(y\)
\(x\times\) 10 = (\(y\times\)30 - \(y\)) + \(x\)\(\times\) 3+ 13
\(x\times\) 10 - \(x\)\(\times\) 3= \(y\) \(\times\)(30-1) +13
\(x\times\) (10 - 3) = \(y\) \(\times\) 29 + 13
\(x\times\) 7 = \(y\times\) 29 + 13
\(x\) = \(\dfrac{y\times29+13}{7}\)
\(x\) = 4\(\times\)\(y\) + \(\dfrac{y+13}{7}\)
\(y\) ≥ 3 ⇒ \(x\) > 4 \(\times\) 3 = 12 (loại) vậy \(y\) = 0; 1; 2 (1)
⇒ \(y\) + 13 \(⋮\) 7 ⇒ \(y\) =1; 8 (2)
từ (1) và(2) ta có: \(y\) = 1
Thay \(y\) = 1 vào biểu thức \(x\) = 4 \(\times\)\(y\)+ \(\dfrac{y+13}{7}\) ta có:
\(x\) = 4 \(\times\) 1 + \(\dfrac{1+13}{7}\)
\(x\) = 4 + 2
\(x\) = 6
Vậy \(x\) = 6; \(y\) = 1
Thử lại ta có: 6,1 = 1,6 \(\times\) 3 + 1,3 (ok)
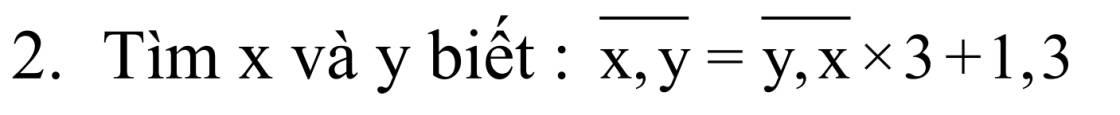 Có bạn nào biết thì chỉ mình với nhé!(Mình cần phần trình bày í)
Có bạn nào biết thì chỉ mình với nhé!(Mình cần phần trình bày í)