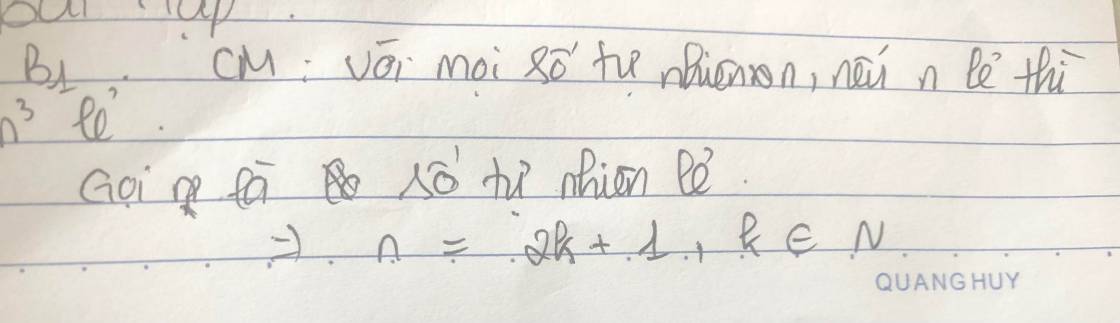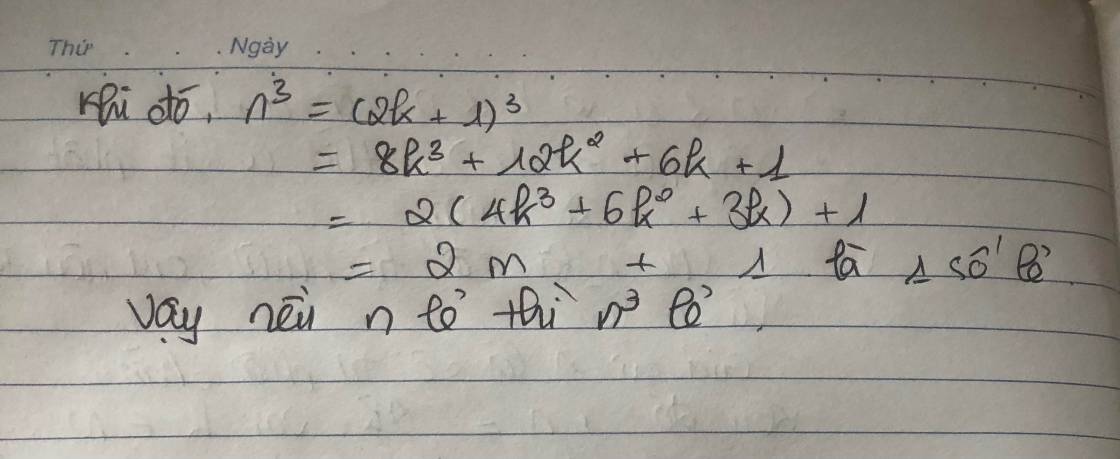Nếu n lẻ thì n3 lẻ
n lẻ <=> n =2k +1 (k ∈ Z)
n^3 =(2k +1)3 =8k3 +3.4k2 +3.2k +1=2( 4k3 +6k2 +3 k) +1
2( 4k3 +6k2 +3 k) chia hết cho 2 => là số chẵn
=>2( 4k3 +6k2 +3 k) +1 là số lẻ => n3 lẻ
Nếu lẻ thì có dạng với .
Do đó .
Suy ra lẻ.
Vậy với mọi số tự nhiên , nếu lẻ thì lẻ.
Đặt n = 2k+1 (k ∈ N)
Khi này: n^3 = (2k+1)^3
= (2k)^3 + 3*(2k)^2*1 + 3*2k*1^2 + 1^3
= 8k^3 + 12k^2 + 6k + 1
= 2 (4k^3 + 6k^2 + 3k) + 1 là số lẻ.
Vậy với mọi số tự nhiên n lẻ thì n^3 lẻ.
Theo bài ra: nếu n lẻ thì n có dạng 2k+1 , k ∈ N
suy ra :n3=(2k+1)3=8k3+12k2+6k+1=2(4k3+6k2+3k)+1 là một số lẻ
Vậy nếu n lẻ thì n3 lẻ
nếu n lẻ thì n^3 lẻ
n lẻ <=>n =2k +1 (k ∈Z)
n^3 =(2k +1)^3 =8k^3 +3.4k^2 +3.2k +1
=2( 4k^3 +6k^2 +3 k) +1
2( 4k^3 +6k^2 +3 k) là số chẵn ;
2( 4k^3 +6k^2 +3 k) +1 là số lẻ => n^3 lẻ
n lẻ => n^2 lẻ => n^3 lẻ
VD : 3 là số lẻ
3 nhân 3 bằng 9,9 là số lẻ
3 nhân 3 nhân 3 bằng 27,27 là số lẻ
Với n là số lẻ ta có :
n là số lẻ nên sẽ có dạng là \(n=2k+1\) \(\left(k\inℕ\right)\)
\(\Rightarrow n^3=\left(2k+1\right)^3\)
\(\Leftrightarrow n^3=8k^3+12k^2+6k+1\)
\(\Leftrightarrow\) \(n^3=2\times\left(4k^3+6k^2+3k\right)+1\)
Mà 2 là số chẵn nên biểu thức \(2\times\left(4k^3+6k^2+3k\right)\) ⋮ \(2\) \(\Rightarrow\) kết quả biểu thức \(2\times\left(4k^3+6k^2+3k\right)\) là một số chẵn
\(\Rightarrow\) \(n^3=2\times\left(4k^3+6k^2+3k\right)+1\) là số lẻ
\(\Rightarrow\) \(n^3\) là một số lẻ
Cho n là 1 số bất kỳ
N chẵn thì lập phương lên cũng bằng lẻ
N lẻ lập phương lên cũng bằng lẻ
=> Với mọi số tự nhiên n,nếu n lẻ thì n3 lẻ
ta có: n lẻ => n=2k+1
=> n3= (2k+1)3 = 8k3+12k2+6k+1 = 2(4k3+3k2+3k)+1 lẻ
=> n3 lẻ
Với n là số lẻ thì n có dạng n= 2k + 1 với k ∈ N.
Từ đó => n3 = ( 2k+ 1)3 = 8k3 + 12k2 + 6k + 1 = 2(4k3 + 6k2 +3k) +1
Vì 2(4k3 + 6k2 +3k) là số chẵn.
nên => 2(4k3 + 6k2 +3k) +1 là số lẻ => n3 là số lẻ.
n thuộc P
n lẻ thì n có công thức là 2k+1 với k thuộc Z
2(K mũ 3 +6K mũ 2 +3k)+1 với k thuộc Z
mà 2 nhân vs số nguyên nào cũng là số chăn
=>2(k mũ 3 +6K mũ 2 +3k) là số chắn
mà số chăn +1 =số lẻ
=> 2( k mũ 3 +6 k mũ 2 +3k) +1 là số lẻ
=> (2k+1) mũ 3 lẻ với k thuộc Z
=>n mũ 3 là số lẻ với n là số tự nhiên
=> với mọi số tự nhiên n, nếu n lẻ thì n mũ 3 lẻ
Đặt n=2k+1
=>n3=(2k+1)3=8k3+3.4k2+3.2k+1=2(4k3+6k2+3k)+1
Mà 2(4k3+6k2+3k) là số chẵn
=>2(4k3+6k2+3k)+1 là số lẻ
=>n3 là số lẻ(ĐPCM)
n lẻ =>n=2k+1 =>n^3=(2k+1)^3=8k^3+12k^2+6k+1=2(4k^3+6k^2+3k)+1 là số lẻ
vậy n lẻ thì n^3 lẻ
Đặt n=2k+1 , ta có :
n3 = (2k+1)3 = 8k3 + 12k2 + 6k2+ 1 = 2(4k2+6k + 3) + 1
mà 2(4k2+6k + 3) là số chẵn => 2(4k2+6k + 3) +1 là số lẻ =>n3 là số lẻ
Giả sử n lẻ (n>0)
n3 = n x n x n = lẻ x lẻ x lẻ = lẻ (tích của các số lẻ luôn là số lẻ)
Với n là số tự nhiên,n=3 mà 3^3=27 => n lẻ thì n^3 lẻ
Gọi n là 2k+1
Ta có: n3= (2k+1)3= 8k3+12k2+6k+1
Vì : 8k3, 12k2; 6k là số chẵn => 8k3+12k2+6k là số chẵn => 8k3+12k2+6k+1 là số lẻ hay n3 là số lẻ
Vậy với mọi số tự nhiên , nếu lẻ thì n3 lẻ ( đpcm )
n là số lẻ nên n=2k+1 ,k là số tự nhiên
n3=\(\left(2k+1\right)^3\)=8k3+12k2+6k+1=2(4k3+6k2+3k)+1
Do k là số tự nhiên nên 2(4k3+6k2+3k) là số chẵn, vậy 2(4k3+6k2+3k)+1 là số lẻ
Hay n3 là số lẻ
Với n lẻ, đặt n = 2k + 1 ( k là số tự nhiên )
=> n^3 = (2k + 1)^3 = 8k^3 + 12k^2 + 6k + 1
Vì 8k^2 + 12k^2 + 6k là số chẵn , 1 lẻ => n^3 lẻ
- Có n là số tự nhiên lẻ, khi đó n = 2k+1; (k ϵ N)
Suy ra n3 = (2k+1)3 = 8k3+3.4k2.1+3.2k.12+1 = 2.(4k3+6k2+3k)+1
=> n3 là số lẻ
- Vậy nếu n lẻ thì n3 lẻ.
nếu n lẻ thì n2=n.n=lẻ => n3=n.n.n=lẻ
ví dụ: 33=3.3.3=27 (là số lẻ)