A) Vẽ t/g ABC (A là góc nhọn), đường cao BH.
1/2.AB.AC.sinA = 1/2.AB.AC.(BH/AB) = 1/2.BH.AC = S(ABC)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Chứng minh:
a, Diện tích của một tam giác bằng nửa tích của hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy
b, Diện tích của tứ giác bất kỳ bằng nửa tích của hai đường chéo nhân với sin của góc nhọn tạo bởi hai đường chéo
chứng minh: diện tích của 1 tam giác bằng nửa tích 2 cạnh nhân với sin góc nhọn tạo bởi 2 đoạn thẳng chứa 2 cạnh ấy
chăm chỉ làm giùm nhe
Chứng minh:Diện tích của 1 tam giác bằng nửa tích 2 cạnh nhân với sin góc nhọn tạo bởi 2 đoạn thẳng chứa 2 cạnh ấy.
1/ CMR nếu hai cạnh của một tam giác có độ dài bằng a và b, góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy bằng \(\alpha\)thì diện tích S của tam giác bằng \(\dfrac{1}{2}absin\alpha\)
Chứng minh rằng : nếu một tam giác có hai cạnh bằng a và b, góc nhọn tạo bởi đường thẳng đó bằng a thì diện tích tam giác đó bằng S=1/2 absina
chứng minh rằng nếu một tam giác có 2 cạnh là a và b , goc nhọn tạo bởi 2 đường thẳng đó là \(\alpha\)thì diện tích của tam giác đó bằng S=\(\frac{1}{2}ab\)\(\sin\alpha\)
Độ dài hai đường chéo của một hình bình hành tỉ lệ với độ dài hai cạnh liên tiếp nó. Chứng minh rằng các góc tạo bởi hai đường chéo bằng các góc của hình bình hành. Giúp mình với ạ. Mình đag cần gấp ạ
Xem chi tiết
Chứng minh nếu 1 tam giác có hai cạnh là a, b, góc nhọn tạo bởi hai cạnh đó là \(\alpha\)thì diện tích tam giác \(=\frac{1}{2}\cdot a\cdot b\cdot\sin\alpha.\)
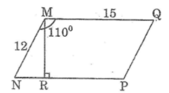
Tính diện tích của hình bình hành có hai cạnh 12cm và 15cm, góc tạo bởi hai cạnh ấy bằng 110 °