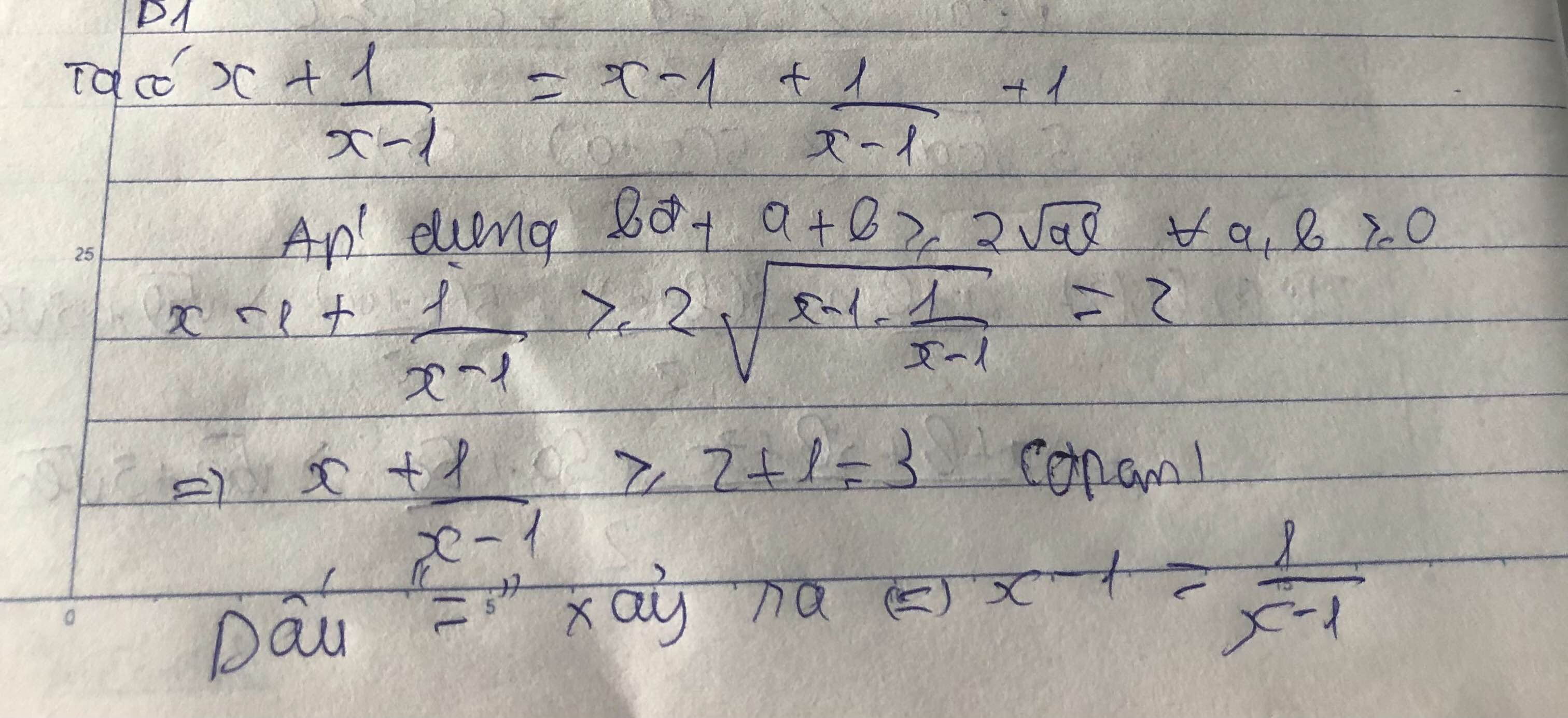Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Áp dụng bất đẳng thức AM-GM ta có :
\(x+\frac{1}{x-1}=\left[\left(x-1\right)+\frac{1}{x-1}\right]+1\ge2\sqrt{\left(x-1\right)\cdot\frac{1}{x-1}}+1=2+1=3\left(đpcm\right)\)
Đẳng thức xảy ra <=> x = 2
Đặt thì và . Ta có
Đẳng thức xảy ra khi và chỉ khi
Đặt t = x -1 thì x = t + 1 và t > 0
Ta có x + 1/x-1 = 1 + t + 1/t ≥1+ 2\(\sqrt{\dfrac{t.1}{t}}\)
Đẳng thức xảy ra khi và chỉ khi t = 1/t =1 suy ra x -1 = 1
\(\Rightarrow\) x = 2
Chứng minh rằng
\(2x+\dfrac{1}{\left(x+1\right)^2}\ge1,\forall x>-1\).
Cho \(x>0\). Chứng minh rằng
\(x+\dfrac{2}{2x+1}\ge\dfrac{3}{2}\).
Cho \(x,y,z\) là ba số dương có tổng bằng 1. Chứng minh rằng
\(\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)\left(1+\frac{1}{z}\right)\ge64\).
Cho x, y là hai số thực dương, chứng mnh rằng \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\).
Cho \(a,b,c\) là ba số dương có tích bằng 1. Chứng minh rằng
\(\dfrac{1}{a^2\left(b+c\right)}+\dfrac{1}{b^2\left(c+a\right)}+\dfrac{1}{c^2\left(a+b\right)}\ge\dfrac{3}{2}\).
Cho \(x,y,z\)là ba số dương có tổng bằng 3. Chứng minh rằng
\(\sqrt{4x+1}+\sqrt{4y+1}+\sqrt{4z+1}\le3\sqrt{5}\).
Cho \(a,b>0\) thỏa mãn điều kiện \(ab\ge1\).
Chứng minh rằng \(\dfrac{a^3}{1+b}+\dfrac{b^3}{1+a}\ge1\).
Cho \(a,b,c\) là ba số dương thỏa mãn \(abc\ge1\). Chứng minh rằng
\(\dfrac{a^3}{\left(1+b\right)\left(1+c\right)}+\dfrac{b^3}{\left(1+c\right)\left(1+a\right)}+\dfrac{c^3}{\left(1+a\right)\left(1+b\right)}\ge\dfrac{3}{4}\).
Cho \(x,y,z\) là ba số dương . Chứng minh rằng
\(x^3+y^3+z^3\ge x^2y+y^2z+z^2x\)
