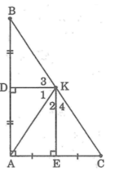
Lấy D đối xứng với A qua M
Xét \(\Delta ABM\)và \(\Delta CDM\)ta có
\(\widehat{M_1}=\widehat{M_2}\)(đối đỉnh)
MB=MC(=\(\frac{1}{2}BC\))
MA=MD (= \(\frac{1}{2}AD\))
=>\(\Delta ABM=\Delta DCM\left(c.g.c\right)\)
=> AB=CD(hai cạnh tương ứng)
\(\widehat{A_1}=\widehat{D_1}\)( hai góc tương ứng)
Mặt khác ta có
\(\widehat{A_1}+\widehat{A_2}=\widehat{BAC}=90^o\)
=>\(\widehat{D_1}+\widehat{A_2}=90^o\)
=>180o-\(\left(\widehat{D_1}+\widehat{A}_2\right)\)=180o-90o
=> \(\widehat{ACD}=90^o\)( tổng 3 góc trong của tam giác ACD)
Xét \(\Delta ABC\)và ta có
\(\widehat{BAC}=\widehat{ACD}=90^o\)
AB=CD(cmt)
AC chung
=> \(\Delta ABC=\Delta CDA\left(c.g.c\right)\)
=>BC=AD (2 cạnh tuong ứng )
Mà theo cách dựng điểm D: MA=MD=\(\frac{1}{2}\)AD
Từ đó ta suy ra AM=\(\frac{1}{2}\)BC
Hay là trong 1 tam giác vuông, trung tuyến ứng với cạnh huyền bằng \(\frac{1}{2}\) cạnh huyền.
sorry hình vẽ hơi xấu