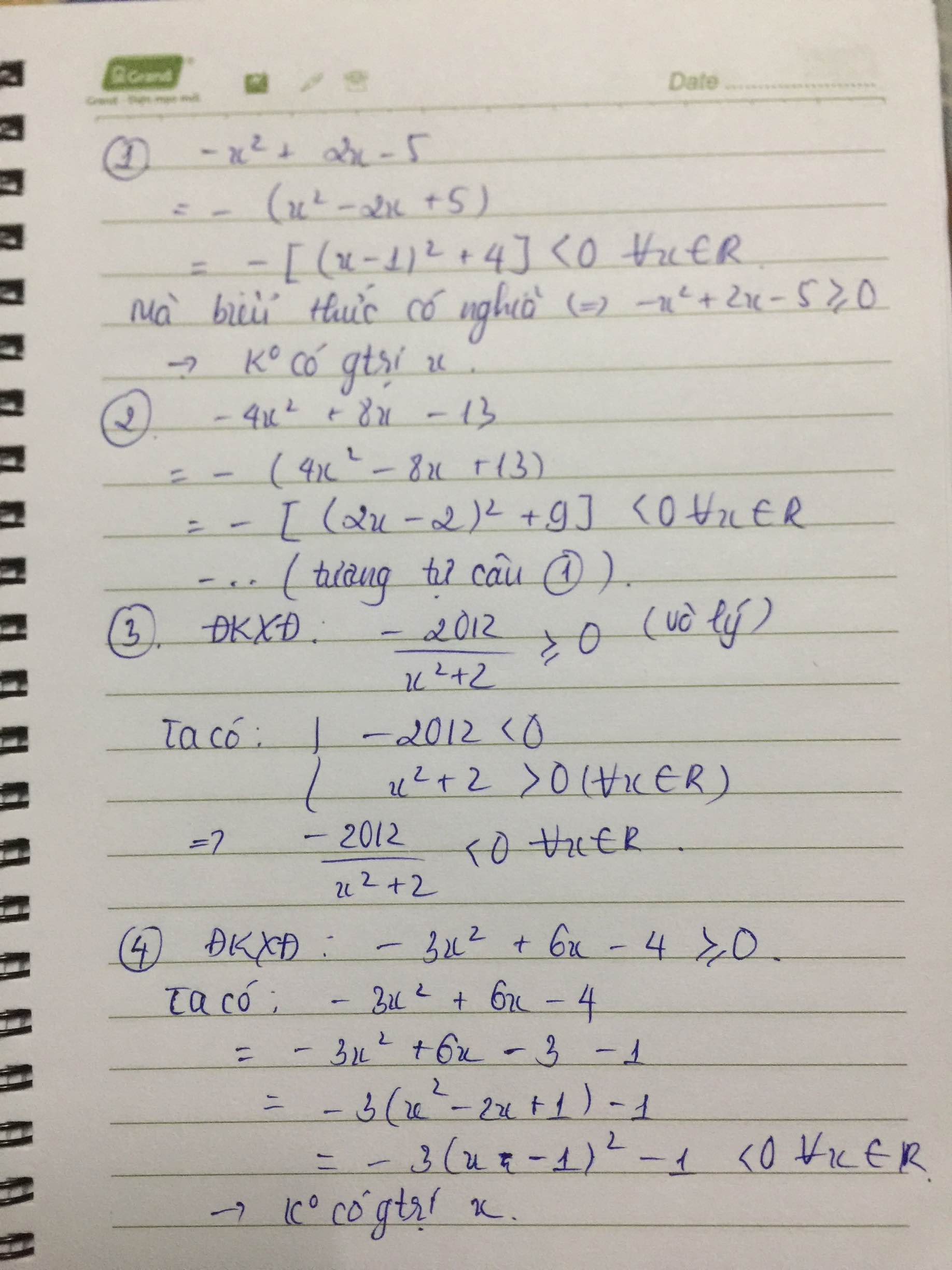a, \(-x^2+2x-5=-\left(x^2-2x+5\right)=-\left(x^2-2x+1+4\right)\)
\(=-\left[\left(x-1\right)^2+4\right]\)
do \(\left(x-1\right)^2\ge0=>\left(x-1\right)^2+4\ge4=>-\left[\left(x-1\right)^2+4\right]\le-4< 0\)
Vậy ko tồn tại..........
b, \(-4x^2+8x-13=-4\left(x^2-2x+\dfrac{13}{4}\right)\)
\(=-4\left[x^2-2x+1+\dfrac{9}{4}\right]=-4\left[\left(x-1\right)^2+\dfrac{9}{4}\right]\le-9< 0\)
vậy....
c, \(\dfrac{-2021}{x^2+2}\) do \(x^2+2>2=>\dfrac{-2012}{x^2+2}< -1006< 0\)
vậy,,,,,,,,,,
d, \(-3x^2+6x-4=-3\left(x^2-2x+\dfrac{4}{3}\right)=-3\left(x^2-2x+1+\dfrac{1}{3}\right)\)
\(=-3\left[\left(x-1\right)^2+\dfrac{1}{3}\right]\le-1< 0\)
vậy...