Biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 xác định khi x – 3 ≠ 0,2x + 3 ≠ 0, x 2 - 3 x ≠ 0 và x 2 - 9 ≠ 0
Suy ra: x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ 3 và x ≠ ± 3
Với điều kiện x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3, ta có:
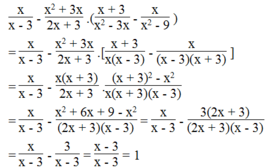
Vậy giá trị của biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 bằng 1 khi x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3


