Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
HA

Chứng minh rằng (7846739-7846738)\(⋮\)7845

Lớp 7 Toán Câu hỏi của OLM

Khách
 
BD
9 tháng 1 2019 lúc 18:53

  7846739-7846738

=7846738x7846-7846738

=7846738x(7846-1)

=7846738x7845  \(⋮\)7845

Bình luận (0)
H24
9 tháng 1 2019 lúc 18:59

Có:

7846739-7884738

=7846738.7846-7846738.1

=7846738.(7846-1)

=7846738.7845\(⋮7845\)

=>\(7846^{739}-7846^{738}⋮7845\)

tk nha!

Bình luận (0)
Các câu hỏi tương tự
KN

Cho ∆CAM có CA = CM. Gọi I là trung điểm của AM. a) Chứng minh rằng: ∆CIA = ∆CIM. b) Chứng minh rằng: CIA=CIM  c) Chứng minh rằng: CI ⊥ AM.

 

Giúp mình với!

Xem chi tiết
Lớp 7 Toán
DD

Cho tam giác ABC cạnh A = 90 độ, phân giác ABC cắt AC tại M, kẻ MD vuông góc với BC, MD cắt AB tại E

a) Chứng minh BA=BD; MA=MD

b) Chứng minh rằng: MB vuông góc với AD

c) Chứng minh rằng: AE=CD

d) Chứng minh rằng:BM vuông góc CE

e) Chứng minh rằng: AD song song CE

Xem chi tiết
Lớp 7 Toán
HL

Cho tam giác ABC. Gọi D, E theo thứ tự là trung điểm của AB, AC.

a) Trên tia đối của tia ED lấy điểm I sao cho EI =ED. Chứng minh rằng AI = DC

b) Chứng minh rằng AI // DC

c) Chứng minh rằng tam giác DAI = tam giác BDC

d) Chứng minh rằng DE = 1/2BC, DE // BC

Xem chi tiết
Lớp 7 Toán
YT

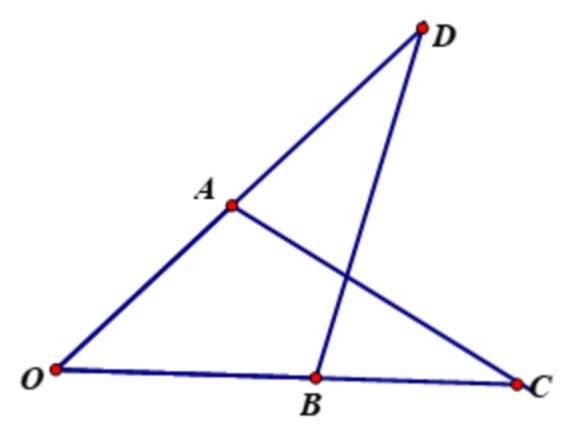
Cho hình vẽ sau, biết OA = OB; góc OAC = góc OBD.

a) Chứng minh rằng AC = BD; OC = OD; AD = BC.

b) Chứng minh rằng tam giác ADC = tam giác BCD.
c) Gọi I là giao điểm của AC và BD. Chứng minh rằng IA = IB và IC = ID.

d) Chứng minh rằng OI là tia phân giác của góc AOB và OI vuông góc CD.

loading...

Xem chi tiết
Lớp 7 Toán
DD

Cho góc xOy nhọn , kẻ Oz là phân giác góc xOy; M thuộc Oz; A thuộc Ox; B thuộc Oy; OA=OB; MA cắt Oy tại C; MB cắt Ox tại D
a) Chứng minh rằng MA=MB
b)Chứng minh rằng OC=OD
c)Chứng minh rằng OM vuông góc AB
d)Chứng minh rằng AB song song với CD

Xem chi tiết
Lớp 7 Toán
ES

Bài 2: 

1.Chứng minh rằng : 9999931999 - 555551997 chia hết cho 5

2.Chứng minh rằng : 1725 - 1321 + 244 Chia hết cho 10

3. Chứng minh rằng: 172008 - 112008 - 32008 + 1 chia hết cho 10

Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM
MT

Cho tam giác ABC vuông cân tại A (Â = 90°, AB = AC). Lấy E € AB
và Fe AC sao cho AE = AF. Đường thẳng đi qua A và vuông góc với BF cắt EC
tại M. Chứng minh rằng:
a) Chứng minh rằng ABAF = ACAE
b) Chứng minh rằng AEMA cân tại M,
c) Chứng minh rằng AAMC cân tại M. Từ đó, hãy suy ra ME = MC.

Xem chi tiết
Lớp 7 Toán
PB
Cho tam giác ABC có ba góc nhọn ABAC. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi I là giao điểm của CD và BE, K là giao điểm của AB và DC  a) Chứng minh rằng  ∆ A D C ∆ A B E   b) Chứng minh rằng:  D I B ^ 60 °  c) Gọi M và N lần lượt là trung điểm của CD và BE. Chứng minh rằng ...
Đọc tiếp
Xem chi tiết
Lớp 7 Toán
NN

Cho tam giác ABC có cạnh AB = AC. Gọi H là trung điểm BC

a) Chứng minh rằng

b) Chứng minh rằng AH là đường trung trực của BC

c) Trên tia đối của tia HA lấy điểm I sao cho HA = HI. Chứng minh rằng IC // AB

d) Chứng minh CAH = CIH

Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM

Khoá học trên OLM (olm.vn)


Khoá học trên OLM (olm.vn)