Với x, y ≠ 0, x ≠ y, ta biến đổi vế trái (VT):
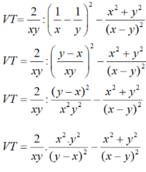
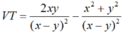
![]()
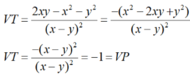
Với x, y ≠ 0, x ≠ y, ta biến đổi vế trái (VT):
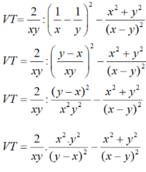
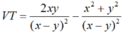
![]()
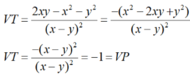
Cho x2+y2 = 2 . Chứng minh rằng :
2(x+1)(y+1) = (x+y)(x+y+2)
chứng minh rằng nếu x^2+y^2+1=xy+x+y thì x=y=1
cho x+y+x=1
x^2+y^2+z^2=1
x^3+y^3+z^3=1
chứng minh rằng x+y^2+x^3=1
chứng minh rằng x^2+y^2+1 >= x*y+x+y
cho x/y+z + y/z+x + z/x+y=1 . Chứng minh rằng x^2/y+z + y^2/z+x + z^2/x+y=0
chứng minh rằng nếu 1/x+1/y+1/z=1 và x=y+z thì 1/x^2+ 1/y^2 +1/z^2 =1
cho x+y=1.chứng minh rằng:3(x^2+y^2)-2(x^3+y^3)=1
Chứng minh rằng với giá trị x và y khác 0 thì biểu thức B=(x+1/x)^2+(y+1/y)^2+(xy+1/xy)^2-(x+1/x)(x+1/y)(xy+1/xy) không phụ thuộc vào x và y
MN giúp mk với ạ...ks ạ...
b1 cho x-y=5 chứng minh rằng x-3y/5-2y=1
b2 cho x^2+y^2/xy=10/3;x>y>0 chứng minh rằng x+y/x-y=2
cho 3 số thực xyz khác 0 thoả mãn (x+y+z)^2=x^2+y^2+z^2 chứng minh rằng 1/x+1/y+1/z=0