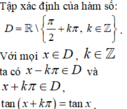
Vậy y= - 3tanx là hàm số tuần hoàn với chu kì π (ứng với k= 1) là số dương nhỏ nhất thỏa tan ( x + k π ) = tan x
Đáp án D
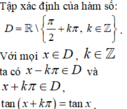
Vậy y= - 3tanx là hàm số tuần hoàn với chu kì π (ứng với k= 1) là số dương nhỏ nhất thỏa tan ( x + k π ) = tan x
Đáp án D
Chu kì của hàm số y = 2 sin ( 2 x + π / 3 ) - 3 cos ( 2 x - π / 4 ) là:
A. 2π
B. π
C. π/2
D. 4 π
Cho các mệnh đề sau
(I) Hàm số f(x) = sin x x 2 + 1 là hàm số chẵn.
(II) Hàm số f(x) = 3sinx + 4cosx có giá trị lớn nhất là 5.
(III) Hàm số f(x) = tanx tuần hoàn với chu kì 2 π .
(IV) Hàm số f(x) = cosx đồng biến trên khoảng (0; π )
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 4
B. 2
C. 3
D. 1
Tìm hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm y = tanx có hoành độ x 0 = π / 4 .
Tìm chu kì của hàm số Y=2cot (x/3+π\4)
Trong các hàm số sau hàm số nào tuần hoàn với chu kỳ π ?
A. y = sin 2x
B. y = tan 2x
C. y = cos x
D. y = cot x 2
Hàm số y = sin ( π / 2 - x ) + c o t x / 3 là hàm tuần hoàn với chu kì:
A. T = π.
B. T = 2π.
C. T = 3π.
D. T = 6π.
Trong bốn hàm số (1)y=cos2x, (2)y=sinx, (3)y=tan2x, (4)y=cot4x có mấy hàm số tuần hoàn với chu kì là π
A. 3
B. 2
C. 0
D. 1
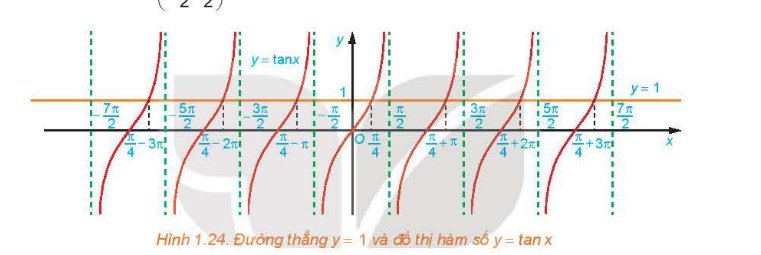
Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn [−π;\(\dfrac{3\pi}{2}\)] để hàm số y=tanx
nhận giá trị âm.
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Tính đạo hàm của hàm số: y = tan π / 2 – x với x ≠ k π , k ∈ Z