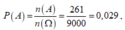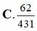Chọn A
Xét phép thử: “Chọn ngẫu nhiên một số tự nhiên trong các số tự nhiên có bốn chữ số”
Ta có ![]()
Biến cố A: “Số được chọn có ít nhất hai chữ số 8 đứng liền nhau”.
Gọi số có 4 chữ số a b c d ¯ là trong đó có ít nhất hai chữ số 8 đứng liền nhau, a ≠ 0
TH1: Có đúng hai chữ số 8 đứng liền nhau.
+) Số có dạng 88 c d ¯ : có 9.9 = 81 số.
+) Số có dạng a 88 d ¯ hoặc a b 88 ¯ : mỗi dạng có 8.9 = 72 số.
TH2: Có đúng ba chữ số 8 trong đó có ít nhất hai chữ số 8 đứng liền nhau.
+) Số có dạng a 888 ¯ : có 8 số.
+) Số có dạng 8 b 88 ¯ hoặc 88 c 8 ¯ hoặc 888 d ¯ : Mỗi dạng có 9 số.
TH3: Cả 4 chữ số đều là chữ số 8: Có 1 số là số 8888
Do đó n(A) = 81 + 2.72 + 8 + 3.9 + 1 = 261
Xác suất cần tìm