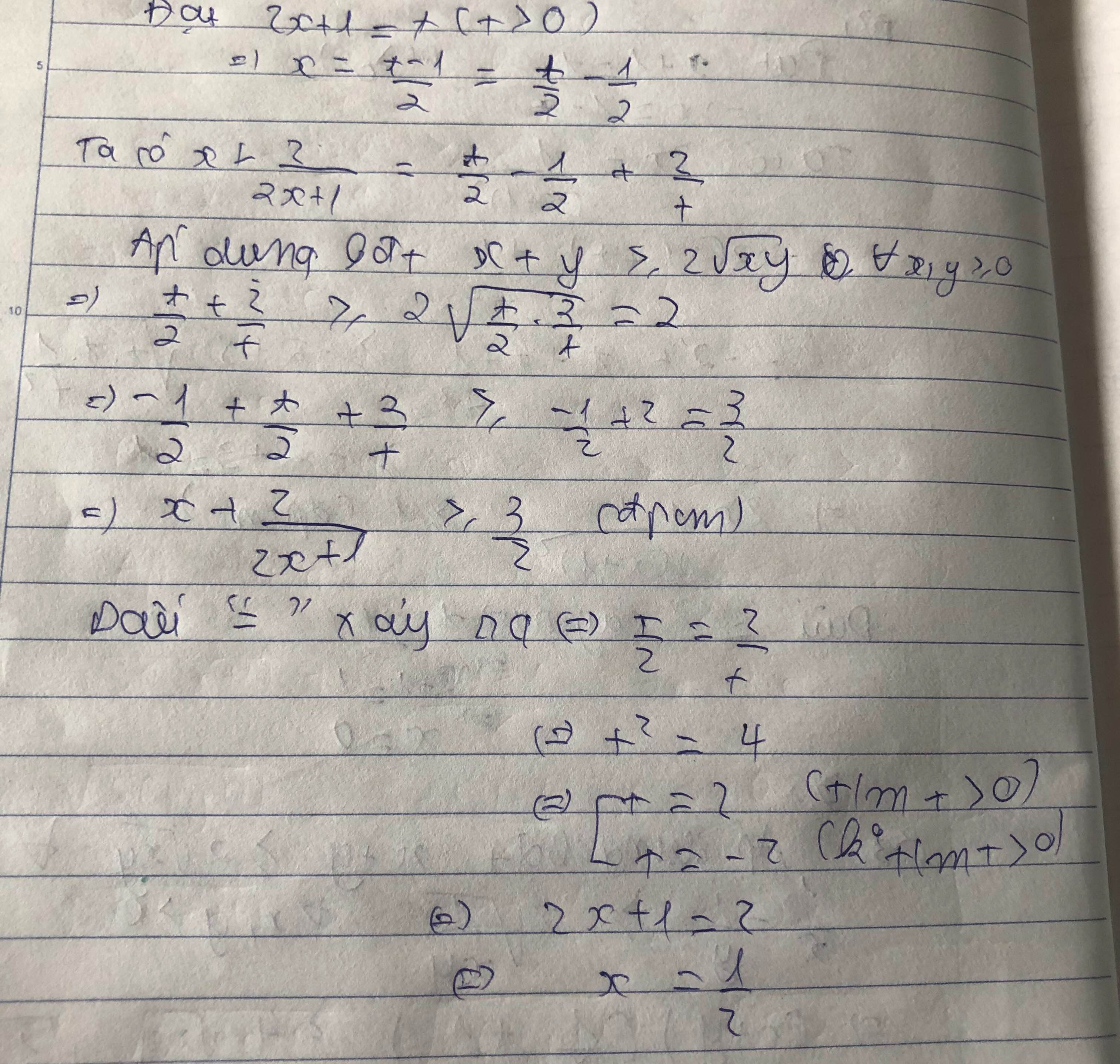Đặt thì và do đó áp dụng bất đẳng thức Cô si ta có
.
Đẳng thức xảy ra khi và chỉ khi .
t/2=2/t
t=2
x=-1/2+1=1/2
Đặt 2x + 1 = t thì t > 0 và x = -1/2+t/2 Ta có
x + 2/2x+1 = -1/2+ t/2+2/t ≥-1/2+ 2 = 3/2
Đẳng thức chỉ xảy ra khi và chỉ khi t/2= 2/t=1 tương đương x = -1/2+ 2/2 = 1/2
Cho \(a,b,c\) là ba số dương có tích bằng 1. Chứng minh rằng
\(\dfrac{1}{a^2\left(b+c\right)}+\dfrac{1}{b^2\left(c+a\right)}+\dfrac{1}{c^2\left(a+b\right)}\ge\dfrac{3}{2}\).
Cho \(a,b,c>0\). Chứng minh rằng
\(\sqrt{\dfrac{a^3}{b^3}}+\sqrt{\dfrac{b^3}{c^3}}+\sqrt{\dfrac{c^3}{a^3}}\ge\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\)
Chứng minh rằng
\(2x+\dfrac{1}{\left(x+1\right)^2}\ge1,\forall x>-1\).
Cho \(a,b,c\) là ba số dương thỏa mãn \(abc\ge1\). Chứng minh rằng
\(\dfrac{a^3}{\left(1+b\right)\left(1+c\right)}+\dfrac{b^3}{\left(1+c\right)\left(1+a\right)}+\dfrac{c^3}{\left(1+a\right)\left(1+b\right)}\ge\dfrac{3}{4}\).
Cho \(a,b,c>0\). Chứng minh rằng
\(\dfrac{ab}{a+b}+\dfrac{bc}{b+c}+\dfrac{ca}{c+a}\le\dfrac{a+b+c}{2}\).
Chứng minh rằng \(x+\dfrac{1}{x-1}\ge3,\forall x>1\).
Cho \(x,y,z\) là ba số dương . Chứng minh rằng
\(x^3+y^3+z^3\ge x^2y+y^2z+z^2x\)
Cho \(a,b>0\) thỏa mãn điều kiện \(ab\ge1\).
Chứng minh rằng \(\dfrac{a^3}{1+b}+\dfrac{b^3}{1+a}\ge1\).
Cho x, y là hai số thực dương, chứng mnh rằng \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\).
