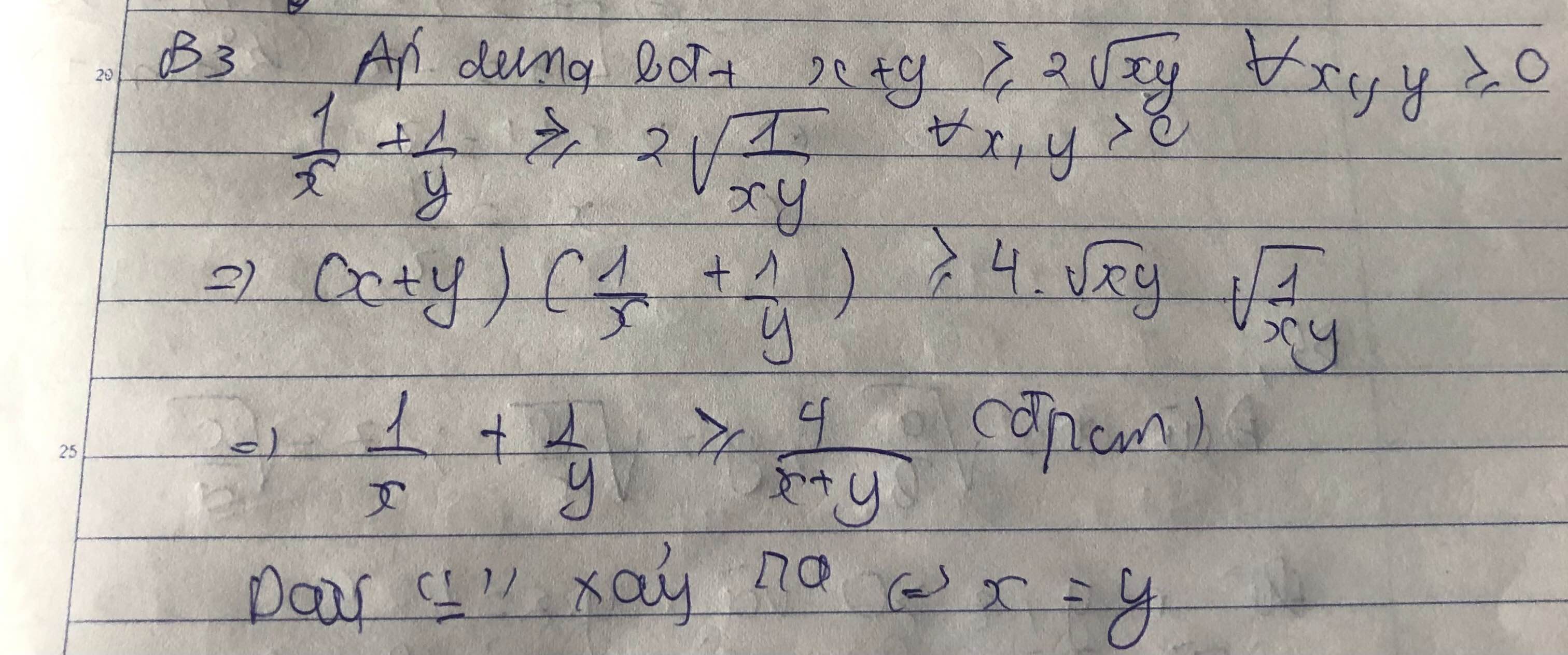Question

Cho x, y là hai số thực dương, chứng mnh rằng \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\).

Answer 1

*Chứng minh bằng biến đổi tương đương

\(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)

<=> \(\frac{x+y}{xy}-\frac{4}{x+y}\ge0\)

<=> \(\frac{\left(x+y\right)^2}{xy\left(x+y\right)}-\frac{4xy}{xy\left(x+y\right)}\ge0\)

<=> \(\frac{x^2+2xy+y^2-4xy}{xy\left(x+y\right)}\ge0\)

<=> \(\frac{\left(x-y\right)^2}{xy\left(x+y\right)}\ge0\)( đúng vì x,y > 0 )

Đẳng thức xảy ra <=> x = y 

Answer 2

*Chứng minh bằng bất đẳng thức

Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có ngay :

\(\frac{1}{x}+\frac{1}{y}\ge\frac{\left(1+1\right)^2}{x+y}=\frac{4}{x+y}\left(đpcm\right)\)

Đẳng thức xảy ra <=> x = y 

Answer 3

*Chứng minh bằng bất đẳng thức

Áp dụng bất đẳng thức AM-GM ta có :

\(x+y\ge2\sqrt{xy}\) ; \(\frac{1}{x}+\frac{1}{y}\ge2\sqrt{\frac{1}{xy}}\)

Nhân vế với vế => \(\left(x+y\right)\left(\frac{1}{x}+\frac{1}{y}\right)\ge4\)=> \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)(đpcm)

Đẳng thức xảy ra <=> x=y

Answer 4

Áp dụng bất đẳng thức Cô si cho hai số dương ta được     x+y\ge2\sqrt{xy}x+y≥2xy​ và  \frac{1}{x}+\frac{1}{y}\ge2\sqrt{\frac{1}{xy}}x1​+y1​≥2xy1​​.

Nhân theo vế hai bất đẳng thức trên với nhau ta được   \left(x+y\right)\left(\frac{1}{x}+\frac{1}{y}\right)\ge4(x+y)(x1​+y1​)≥4 hay   \frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}x1​+y1​≥x+y4​.

Đẳng thức xảy ra khi và chỉ khi  $x=y$.

Answer 5

x=y

Answer 6

Áp dụng bất đẳng thức Cô si cho 2 số dương ta có x + y ≥2\(\sqrt{xy}\)

và  1/x + 1/y ≥ 4/x+y

BĐT xảy ra khi và chỉ khi x = y

Answer 7

Answer 8

Answer 9