Các câu hỏi tương tự
Cho tứ giác MNPQ. Gọi E,F,G,H lần lượt là trung điểm của các cạnh MN, NP, PQ, QM. Chứng minh: EFGH là hình bình hành
Cho tứ giác MNPQ. Gọi E, F , G, H lần lượt là trung điểm các cạnh MN, NP, PQ, QM. Tứ giác EFGH là hình thoi nếu 2 đường chéo MP, NQ của tứ giác MNPQ:
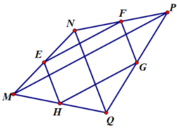
A. Bằng nhau
B. Vuông góc
C. Vuông góc với nhau tại trung điểm mỗi đường
D. Cắt nhau tại trung điểm mỗi đường.
Cho tử giác MNPQ. Gọi E. F. G. H lần lượt là trung điểm của các cạnh MN. NP PQ. QM CMR: Tử giác EFGH là hình bình hành.
Cho tử giác MNPQ. Gọi E. F. G. H lần lượt là trung điểm của các cạnh MN. NP PQ. QM CMR Tử giác EFGH là hình bình hành.
Cho tứ giác MNPQ, gọi A, B, C, D lần lượt là trung điểm của MN, NP, PQ, QM. Chứng minh tứ giác ABCD là hình bình hành.
Cho tứ giác MNPQ có E, F, G, H lần lượt là trung điểm của các cạnh MN,NP.PQ.PM.
a) Chứng Minh rằng EFGH là hình bình hành
b) Hai đường chéo của tứ giác MNPQ phải có điều kiện gid thì tứ giác EFGH là hình thang. Vẽ hình minh họa.
cho tứ giác MNPQ, điểm A,B,C,D lần lượt là trung điểm của các cạnh MN,NP,PQ, QM. CMR tứ giác ABCD là hình bình hành
cho tứ giác MNPQ,gọi H K I G lần lượt là trung điểm của các cạnh MN,NP PQ QM a.tứ giác HKIG là hình gì?vì sao? b.tứ giác MNPQ có thêm điều kiện gì thì tứ giác HKIG là hình chữ nhật ?vì sao?
cho tứ giác MNPQ có NP=MQ và NP không song song với MQ. Gọi A,B,C,D,E,F lần lượt là trung điểm của các đoạn thẳng MN,NP,PQ,QM,MP.NP
a, chứng minh tứ giác AFCE là hình thoi
b, chứng minh AC,BD,EF cùng cắt nhau tại trung điểm


