Cho tứ giác ABCD có AC và BD căt nhau tại O. Một điểm S không thuộc mp (ABCD). Trên đoạn SC lấy 1 điểm M không trùng với S và C. Giao điểm của đường thẳng SD với mặt phẳng (ABM) là
A. giao điểm của SD và BA
B. Giao điểm của SD và AM
C. Giao điểm của SD và BK. ( K là giao điểm của SO và AM)
D. giao điểm của SD và MK ( với K là giao điểm của SO và AM)
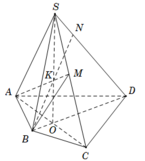
+ Chọn mặt phẳng phụ (SBD) chứa SD.
+ Tìm giao tuyến của hai mặt phẳng (SBD) và (AMB).
Ta có B là điểm chung thứ nhất của 2 mp đó.
Trong mặt phẳng (SAC), gọi K là giao điểm của AM và SO.
Ta có:
+ K thuộc SO mà S O ⊂ S B D suy ra K ∈ S B D
+ K thuộc AM mà A M ⊂ A B M suy ra K ∈ A B M
Suy ra K là điểm chung thứ hai của (SBD) và (ABM).
Do đó giao tuyến của 2 mp này là: BK..
+ Trong mặt phẳng (SBD), gọi SD và BK cắt nhau tại N. Ta có:
▪ N thuộc BK mà B K ⊂ A B M suy ra N ∈ A B M .
▪ N thuộc SD
Vậy giao điểm của SD và (ABM) là N.
Chọn C.

