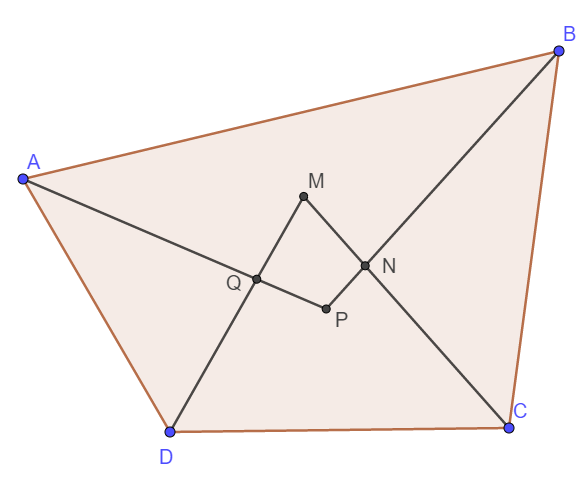
Gọi giao điểm các đường phân giác trong tứ giác ABCD lần lượt là M, N, P, Q như hình vẽ bên trên.
Xét tam giác APB có: \(\widehat{APB}=180^o-\widehat{PAB}-\widehat{PBA}=\frac{360^o-\widehat{DAB}-\widehat{CBA}}{2}\)
Tương tự xét tam giác MCD ta cũng có:
\(\widehat{DMC}=\frac{360^o-\widehat{ADC}-\widehat{BCD}}{2}\)
Suy ra \(\widehat{QMN}+\widehat{QPN}=\frac{360^o-\widehat{ADC}-\widehat{BCD}}{2}+\frac{360^o-\widehat{DAB}-\widehat{ABC}}{2}\)
\(=\frac{720^o-360^o}{2}=180^o\)
Do tổng 4 góc trong một tứ giác bằng 360o nên ta cũng có \(\widehat{MQP}+\widehat{MNP}=360^o-180^o=180^o\)
Vậy tứ giác MNPQ có các góc đối bù nhau.

