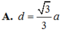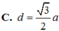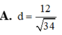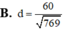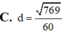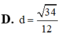Đáp án B
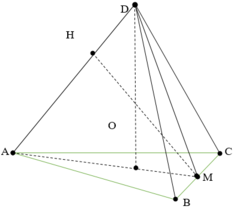
Gọi O là trọng tâm ∆ABC
Kẻ AM ⊥ AC và MH ⊥ AD
Vì DABC là tứ diện đều => DO ⊥ (ABC)
Vì ∆ABC đều => AO = ![]()
Xét ∆DAO vuông tại O

Ta có: DO ⊥ BC và AM ⊥ BC
=> (DAM) ⊥ BC
=> MH ⊥ BC
Lại có MH ⊥ DA
=> MH = d(BC, DA)
Xét ∆DAM, ta có:
DO.AM = MH.AD
⇔ MH = a 2 2
⇔ d(BC, DA) = a 2 2