Đáp án C.
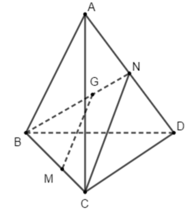
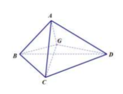
+ Gọi G 0 là trọng tâm tam giác BCD=> G B ⇀ + G C ⇀ + G D ⇀ = 3 G G 0 ⇀
=>
G
A
⇀
+
G
B
⇀
+
G
C
⇀
+
G
D
⇀
=
0
⇀
![]()
=> A, G, G 0 thẳng hàng ⇒ G 0 = G A
+ Có A, G,
G
A
thẳng hàng mà ![]()