Các câu hỏi tương tự
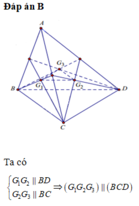
Cho tứ diện ABCD. gọi G₁, G₂ là trọng tâm ∆ABD và ∆ACD. C/m: G₁ G₂ // (ABC) G₁ G₂ // (BCD)
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng:
A. GE//CD
B. GE và CD chéo nhau
C. GE cắt AD
D. GE cắt CD
Trong mặt phẳng tọa độOxy, cho 3 điểm A(1;0), B(-1;5), C(3;4). Gọi G là trọng tâm của tam giác ABC. Tìm tọa độ điểm G' là ảnh của G qua việc thực hiện liên tiếp phép tịnh tiến theo véc tơ u (2; 3) và phép vị tự tâm C, tỉ số k=-3
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB 2MC. Mệnh đề nào sau đây đúng? A.
M
G
∥
(
B
C
D
)
B.
M
G
∥
(
A
C
D
)
C.
M
G
∥
(
A...
Đọc tiếp
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB = 2MC. Mệnh đề nào sau đây đúng?
A. M G ∥ ( B C D )
B. M G ∥ ( A C D )
C. M G ∥ ( A B D )
D. M G ∥ ( A B C )
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là: A. B. C. D.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
A. ![]()
B. ![]()
C. ![]()
D. 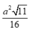
Trong hệ tọa độ Oxy cho tam giác ABC có A(3 ; 5) ; B( 1 ;2) và C( 5 ;2). Tìm tọa độ trọng tâm G của tam giác ABC ? A. G( -9 ; -9) B. C. G( 3 ;3) D.G(9 ; 9)
Đọc tiếp
Trong hệ tọa độ Oxy cho tam giác ABC có A(3 ; 5) ; B( 1 ;2) và C( 5 ;2). Tìm tọa độ trọng tâm G của tam giác ABC ?
A. G( -9 ; -9)
B. 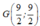
C. G( 3 ;3)
D.G(9 ; 9)
Cho tứ diện ABCD, G là trọng tâm của tam giác ABD, M là điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?
A. MG // (ACD)
B. MG // (ABC)
C. MG // AB
D. MG cắt AC
Cho tứ diện ABCD với G là trọng tâm của tam giác ABD, M là điểm trên cạnh BC sao cho . Khi đó mệnh đề nào sau đây là đúng?
A. MG cắt CD.
B. MG//CD.
C. MG//(ACD)
D. MG cắt BD.
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.
Phép vị tự tâm G tỉ số -1/2 biến tam giác ABC thành
A. Tam giác GBC
B. Tam giác DEF
C. Tam giác AEF
D. Tam giác AFE
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. M thuộc đoạn thẳng BC sao cho BM = 2MC. Giao tuyến của mặt phẳng (BGM) và (ACD)