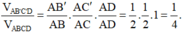Các câu hỏi tương tự
Cho tứ diên ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ diện A'B'C'D' và khối tứ diện ABCD bằng:
A. 1 8
B. 1 6
C. 1 4
D. 1 2
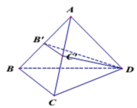
Cho tứ diện ABCD. Gọi B ' , C ' lần lượt là trung điểm của AB và CD. Khi đó, tỷ số thể tích của khối đa diện A B ' C ' D và khối đa diện ABCD bằng
A. 1/8
B. 1/6
C. 1/4
D. 1/2
Cho khối tứ diện ABCD. Gọi M, N, E lần lượt là trung điểm của AB, BD, DA. Tỉ số thể tích của khối tứ diện MNEC và ABCD bằng: A. 1/4 B. 1/8 C. 1/2 D. 1/3
Đọc tiếp
Cho khối tứ diện ABCD. Gọi M, N, E lần lượt là trung điểm của AB, BD, DA. Tỉ số thể tích của khối tứ diện MNEC và ABCD bằng:
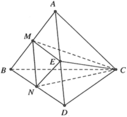
A. 1/4
B. 1/8
C. 1/2
D. 1/3
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V A.
11
2
a
3
216
B.
7...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 8
D. 13 2 a 3 216
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V. A.
11
2
a
3
216
B.
7
2...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 18
D. 13 2 a 3 216
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B, C, D sao cho thể tích của khối tứ diện ABCD nhỏ nhất và
A
B
A
B
+
A
C
A
C
+
A...
Đọc tiếp
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B', C', D' sao cho thể tích của khối tứ diện AB'C'D' nhỏ nhất và A B A B ' + A C A C ' + A D A D ' = 4 . Tìm phương trình của mặt phẳng (B’C’D’)
A. 16 x + 40 y - 44 z + 39 = 0
B. 16 x - 40 y - 44 z + 39 = 0
C. 16 x + 40 y + 44 z + 39 = 0
D. 16 x + 40 y - 44 z - 39 = 0
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, ADlần lượt lấy các điểm B’,C’,D’ sao cho
A
B
A
B
+
A
C
A
C
+
A
D...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, ADlần lượt lấy các điểm B’,C’,D’ sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện AB’C’D’ có thể tích nhỏ nhất. Phương trình mặt phẳng (B’C’D’) là
A. 16x-40y-44z-39=0.
B. 16x-40y-44z+39=0.
C. 16x+40y+44z-39=0.
D. 16x+40y-44z+39=0.
Cho hình vuông ABCD có cạnh bằng 6 cm. Gọi E, F lần lượt là trung điểm của các cạnh AB và AD. Gấp hình vuông trên để được tứ diện ACEF. Thể tích khối tứ diện ACEF là A. 18
cm
3
. B. 3
cm
3
. C. 27
cm
3
. D. 9
cm
3
.
Đọc tiếp
Cho hình vuông ABCD có cạnh bằng 6 cm. Gọi E, F lần lượt là trung điểm của các cạnh AB và AD. Gấp hình vuông trên để được tứ diện ACEF. Thể tích khối tứ diện ACEF là
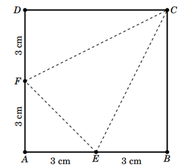
A. 18 cm 3 .
B. 3 cm 3 .
C. 27 cm 3 .
D. 9 cm 3 .
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T) A.
S
a
2
2
B.
S
a
2
3
6
C. ...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
A. S = a 2 2
B. S = a 2 3 6
C. S = a 2 3 9
D. S = a 2 6